2016-2017学年山东省枣庄市滕州市九年级上学期期末数学试卷
试卷更新日期:2017-03-13 类型:期末考试
一、选择题:
-
1. 已知反比例函数y= 的图象经过点P(﹣1,2),则这个函数的图象位于( )A、第一、三象限 B、第二、三象限 C、第二、四象限 D、第三、四象限2. 下列性质中,菱形具有矩形不一定具有的是( )A、对角线相等 B、对角线互相平分 C、邻边互相垂直 D、对角线互相垂直3. 随州市尚市“桃花节”观赏人数逐年增加,据有关部门统计,2014年约为20万人次,2016年约为28.8万人次,设观赏人数年均增长率为x,则下列方程中正确的是( )A、20(1+2x)=28.8 B、28.8(1+x)2=20 C、20(1+x)2=28.8 D、20+20(1+x)+20(1+x)2=28.84. 三张外观相同的卡片分别标有数字1、2、3,从中随机一次抽出两张,这两张卡片上的数字恰好都小于3的概率是( )A、 B、 C、 D、5. 关于x的一元二次方程x2﹣ x+sinα=0有两个相等的实数根,则锐角α等于( )A、15° B、30° C、45° D、60°6. 在Rt△ABC中,∠A、∠B、∠C对边分别为a、b、c,∠C=90°,若sinA= ,则cosB等于( )A、 B、 C、 D、7. 图中三视图对应的几何体是( )
 A、
A、 B、
B、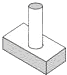 C、
C、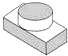 D、
D、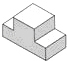 8. 如图,为了估计荆河的宽度,在荆河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R,如果QS=60m,ST=120m,QR=80m,则荆河的宽度PQ为( )
8. 如图,为了估计荆河的宽度,在荆河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R,如果QS=60m,ST=120m,QR=80m,则荆河的宽度PQ为( ) A、40m B、120m C、60m D、180m9. 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不一定相似的是( )
A、40m B、120m C、60m D、180m9. 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不一定相似的是( ) A、
A、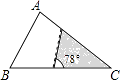 B、
B、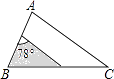 C、
C、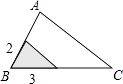 D、
D、 10. 如图,一艘海轮位于灯塔P的东北方向,距离灯塔40 海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则海轮行驶的路程AB为( )海里.
10. 如图,一艘海轮位于灯塔P的东北方向,距离灯塔40 海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则海轮行驶的路程AB为( )海里.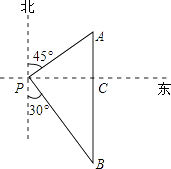 A、40+40 B、80 C、40+20 D、8011. 已知点A(x1 , y1)、B(x2 , y2)是反比例函数y=﹣ 图象上的两点,若x2<0<x1 , 则有( )A、0<y1<y2 B、0<y2<y1 C、y2<0<y1 D、y1<0<y212. 已知二次函数 (a≠0)与一次函数y2=kx+m(k≠0)的图象交于点A(﹣2,4),B(8,2),如图所示,则能使y1>y2成立的x的取值范围是( )
A、40+40 B、80 C、40+20 D、8011. 已知点A(x1 , y1)、B(x2 , y2)是反比例函数y=﹣ 图象上的两点,若x2<0<x1 , 则有( )A、0<y1<y2 B、0<y2<y1 C、y2<0<y1 D、y1<0<y212. 已知二次函数 (a≠0)与一次函数y2=kx+m(k≠0)的图象交于点A(﹣2,4),B(8,2),如图所示,则能使y1>y2成立的x的取值范围是( )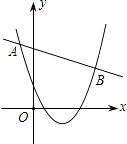 A、x<﹣2 B、x>8 C、﹣2<x<8 D、x<﹣2或x>813. 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
A、x<﹣2 B、x>8 C、﹣2<x<8 D、x<﹣2或x>813. 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )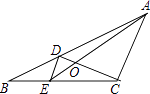 A、1:3 B、1:4 C、1:5 D、1:25
A、1:3 B、1:4 C、1:5 D、1:25二、填空题
-
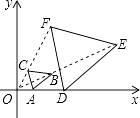
14. 如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE= .
 15. 如图,直角三角形纸片的两直角边长分别为4,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是 .
15. 如图,直角三角形纸片的两直角边长分别为4,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是 .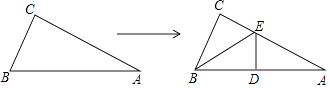 16. 将抛物线y=3(x﹣4)2+2向右平移1个单位长度,再向下平移3个单位长度,平移后抛物线的解析式是 .17. 如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点D的坐标是 .
16. 将抛物线y=3(x﹣4)2+2向右平移1个单位长度,再向下平移3个单位长度,平移后抛物线的解析式是 .17. 如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点D的坐标是 .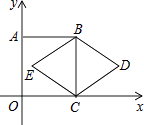 18. 如图,点A是反比例函数y1= (x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2= (x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为 .
18. 如图,点A是反比例函数y1= (x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2= (x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为 . 19. 抛物线y=ax2+bx+c(a≠0)图象的一部分如图所示,其对称轴为x=2,与x轴的一个交点是(﹣1,0),有以下结论:①abc>0;②4a﹣2b+c<0;③4a+b=0④抛物线与x轴的另一个交点是(5,0)⑤若点(﹣3,y1)(﹣6,y2)都在抛物线上,则y1<y2 . 其中正确的是 . (只填序号)
19. 抛物线y=ax2+bx+c(a≠0)图象的一部分如图所示,其对称轴为x=2,与x轴的一个交点是(﹣1,0),有以下结论:①abc>0;②4a﹣2b+c<0;③4a+b=0④抛物线与x轴的另一个交点是(5,0)⑤若点(﹣3,y1)(﹣6,y2)都在抛物线上,则y1<y2 . 其中正确的是 . (只填序号)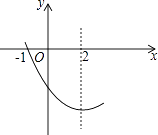
三、解答题
-
20. 计算:sin230°+2sin60°﹣tan45°﹣tan60°+cos230°.21. 某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.(1)、该顾客至少可得到元购物券,至多可得到元购物券;(2)、请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.22. 如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
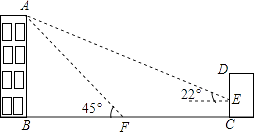
(参考数据:sin22°≈ ,cos22° ,tan22 )
(1)、求办公楼AB的高度;(2)、若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.23. 某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)、求y与x之间的函数关系式;(2)、当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?24. 如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E,H分别在AB、AC上,已知BC=40cm,AD=30cm.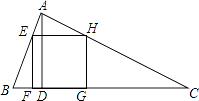 (1)、求证:△AEH∽△ABC;(2)、求这个正方形的边长与周长.25. 如图,四边形ABCD为正方形,点A坐标为(0,1),点B坐标为(0,﹣2),反比例函数y= 的图象经过点C,一次函数y=ax+b的图象经过A,C两点.
(1)、求证:△AEH∽△ABC;(2)、求这个正方形的边长与周长.25. 如图,四边形ABCD为正方形,点A坐标为(0,1),点B坐标为(0,﹣2),反比例函数y= 的图象经过点C,一次函数y=ax+b的图象经过A,C两点.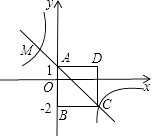 (1)、求反比例函数与一次函数的解析式;(2)、若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.26. 如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)、求反比例函数与一次函数的解析式;(2)、若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.26. 如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.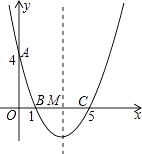 (1)、求抛物线的解析式和对称轴;(2)、在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)、连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式和对称轴;(2)、在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)、连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.