2016-2017学年四川省雅安市八年级上学期期末数学试卷

试卷更新日期：2017-03-13 类型：期末考试

进入出卷网下载

一、选择题

1. 在直角坐标中，点（﹣1，2）第（）象限．

A、一 B、二 C、三 D、四

查看试题解析
2. $\sqrt{25}$ 的相反数是（）

A、5 B、﹣5 C、±5 D、25

查看试题解析
3. 在给出的一组数0，π， $\sqrt{5}$ ， 3.14， $\sqrt[3]{9}$ ， $\frac{22}{7}$ 中，无理数有（　　）

A、1个 B、2个 C、3个 D、5个

查看试题解析
4. 已知 ${\begin{matrix} x = 2 k \\ y = - 3 k \end{matrix}$ 是二元一次方程2x﹣y=14的解，则k的值是（）

A、2 B、﹣2 C、3 D、﹣3

查看试题解析
5. 下列各式中，正确的是（）

A、 $\sqrt{16}$ =±4 B、± $\sqrt{16}$ =4 C、 $\sqrt[3]{- 27}$ =﹣3 D、 $\sqrt{{(- 4)}^{2}}$ =﹣4

查看试题解析
6. 如图，直线a∥b，AC⊥AB，AC交直线b于点C，∠1=60°，则∠2的度数是（）

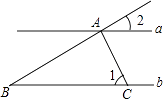A、50° B、45° C、35° D、30°

查看试题解析
7. 某班50名同学的数学成绩为：5人100分，30人90分，10人75分，5人60分，则这组数据的众数和平均数分别是（）

A、90，85 B、30，85 C、30，90 D、90，82

查看试题解析
8. 将三角形三个顶点的横坐标都减2，纵坐标不变，则所得三角形与原三角形的关系是（）

A、将原三角形向左平移两个单位 B、将原三角形向右平移两个单位 C、关于x轴对称 D、关于y轴对称

查看试题解析
9. 下列命题中，真命题有（）
①同旁内角互补；
②三角形的一个外角等于它的两个内角之和；
③一个三角形的最大角不会小于60°，最小角不会大于60°；
④若函数y=（m+1）x $^{m^{2} - 3}$ 是正比例函数，且图象在第二、四象限，则m=﹣2．

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 对于一次函数y=x+6，下列结论错误的是（）

A、y随x的增大而增大 B、函数图象与坐标轴围成的三角形面积为18 C、函数图象不经过第四象限 D、函数图象与x轴正方形夹角为30°

查看试题解析
11.
在平面直角坐标系中，已知点A（2，3），B（6，3），连接AB，如果点P在直线y=x﹣1上，且点P到直线AB的距离小于1，那么称点P是线段AB的“临近点”，则下列点为AB的“临近点”的是（）

A、（ $\frac{7}{2}$ ， $\frac{5}{2}$ ） B、（3，3） C、（6，5） D、（1，0）

查看试题解析
12. 如图，直线y=﹣ $\frac{1}{2}$ x+3与坐标轴分别交于A，B两点，与直线y=x交于点C，线段OA上的点Q以每秒1个单位长度的速度从点O出发向点A作匀速运动，运动时间为t秒，连接CQ．若△OQC是等腰直角三角形，则t的值为（）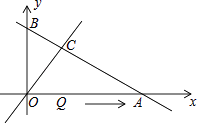

A、2 B、4 C、2或3 D、2或4

查看试题解析

二、填空题

13. 边长为2 $\sqrt{2}$ 的正方形的对角线长为．

查看试题解析
14. 在平面直角坐标系中，点M（2+x，9﹣x²）在x轴的负半轴上，则点M的坐标是．

查看试题解析
15. 已知关于x，y的二元一次方程组 ${\begin{matrix} a x - y + b = 0 \\ y = k x \end{matrix}$ （a，b，k均为常数，且a≠0，k≠0）的解为 ${\begin{matrix} x = - 4 \\ y = - 2 \end{matrix}$ ，则直线y=ax+b和直线y=kx的交点坐标为．

查看试题解析
16. 当三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”．如果一个“特征三角形”的“特征角”为100°，那么这个“特征三角形”的最小内角的度数为．

查看试题解析
17. 已知y= $\sqrt{x - 1}$ ﹣ $\sqrt{1 - x}$ +4，则 $\sqrt{x^{2} y}$ = ．

查看试题解析

三、解答题

18. 计算

(1)、2 $\sqrt{3}$ ﹣ $\sqrt{8}$ ﹣ $\frac{1}{2}$ $\sqrt{48}$ +（ $\sqrt{2}$ +1）² ．

(2)、 $\frac{\sqrt{20} + \sqrt{5}}{\sqrt{5}}$ ﹣ $\sqrt{\frac{1}{3}}$ × $\sqrt{12}$ +（ $\sqrt{3}$ + $\sqrt{2}$ ）（ $\sqrt{3}$ ﹣ $\sqrt{2}$ ）．

查看试题解析
19. 如图，∠C=∠1，∠2与∠D互余，BE⊥DF，垂足为G．求证：AB∥CD．

查看试题解析
20. 某商场代销甲、乙两种商品，其中甲种商品进价为120元/件，售价为130元/件，乙种商品进价为100元/件，售价为150元/件．

(1)、若商场用36000元购进这两种商品若干，销售完后可获利润6000元，则该商场购进甲、乙两种商品各多少件？（列方程组解答）

(2)、若商场购进这两种商品共100件，设购进甲种商品x件，两种商品销售后可获总利润为y元，请写出y与x的函数关系式（不要求写出自变量x的范围），并指出购进甲种商品件数x逐渐增加时，总利润y是增加还是减少？

查看试题解析
21. 某校八年级学生开展踢毽子比赛活动，每班派5名学生参加，按团体总分多少排列名次，在规定时间内每人踢100个以上（含100）为优秀，下表是成绩最好的甲班和乙班5名学生的比赛数据（单位：个）
1号
2号
3号
4号
5号
总分
甲班
89
100
96
118
97
500
乙班
100
95
110
91
104
500
统计发现两班总分相等，此时有学生建议，可以通过考查数据中的其他信息作为参考，请解答下列问题：

(1)、计算两班的优秀率；

(2)、求两班比赛数据的中位数；

(3)、计算两班比赛数据的方差；

(4)、你认为应该定哪一个班为冠军？为什么？

查看试题解析
22. 在平面直角坐标系中，O为坐标原点，点A的坐标为（2x+y﹣3，x﹣2y），它关于x轴的对称点A₁的坐标为（x+3，y﹣4），关于y轴的对称点为A₂ ．

(1)、求A₁、A₂的坐标；

(2)、证明：O为线段A₁A₂的中点．

查看试题解析
23. 在△ABC中，已知AB=AC=10，BC=16，点D在BC上，且BD= $\frac{7}{2}$ ，连接AD，求证：AD⊥AC．

查看试题解析
24.
如图，一次函数y=ax﹣b与正比例函数y=kx的图象交于第三象限内的点A，与y轴交于B（0，﹣4），且OA=AB，△AOB的面积为6．

(1)、求两个函数的解析式；

(2)、若有一个点M（2，0），直线BM与AO交于点P，求点P的坐标；

(3)、在x轴上是否存在点E，使S_△_ABE=5？若存在，求点E的坐标；若不存在，请说明理由．

查看试题解析

	1号	2号	3号	4号	5号	总分
甲班	89	100	96	118	97	500
乙班	100	95	110	91	104	500