2016-2017学年山东省青岛市黄岛区九年级上学期期末数学试卷
试卷更新日期:2017-03-13 类型:期末考试
一、选择题
-
1. 下面四个几何体中,其主视图为圆形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在△ABC中,∠C=90°,AB=5,BC=3,则sinB的值是( )A、 B、 C、 D、3. 抛物线y=x2﹣2x+3的顶点坐标是( )A、(1,3) B、(﹣1,3) C、(1,2) D、(﹣1,2)4. 甲、乙两名同学在一次用频率去估计概率的实验中,统一了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )
2. 在△ABC中,∠C=90°,AB=5,BC=3,则sinB的值是( )A、 B、 C、 D、3. 抛物线y=x2﹣2x+3的顶点坐标是( )A、(1,3) B、(﹣1,3) C、(1,2) D、(﹣1,2)4. 甲、乙两名同学在一次用频率去估计概率的实验中,统一了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )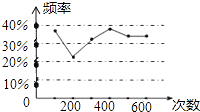 A、从一个装有2个白球和1个红球的袋子中任取两球,取到两个白球的概率 B、任意写一个正整数,它能被2整除的概率 C、抛一枚硬币,连续两次出现正面的概率 D、掷一枚正六面体的骰子,出现1点的概率5. 已知点(﹣2,y1),(﹣1,y2),(1,y3)都在反比例函数y= (k<0)的图象上,那么y1 , y2与y3的大小关系是( )A、y3<y1<y2 B、y3<y2<y1 C、y1<y2<y3 D、y1<y3<y26. 如图,已知小鱼与大鱼是位似图形,则小鱼的点(a,b)对应大鱼的点( )
A、从一个装有2个白球和1个红球的袋子中任取两球,取到两个白球的概率 B、任意写一个正整数,它能被2整除的概率 C、抛一枚硬币,连续两次出现正面的概率 D、掷一枚正六面体的骰子,出现1点的概率5. 已知点(﹣2,y1),(﹣1,y2),(1,y3)都在反比例函数y= (k<0)的图象上,那么y1 , y2与y3的大小关系是( )A、y3<y1<y2 B、y3<y2<y1 C、y1<y2<y3 D、y1<y3<y26. 如图,已知小鱼与大鱼是位似图形,则小鱼的点(a,b)对应大鱼的点( )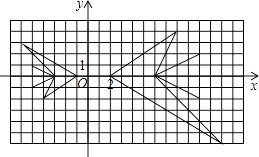 A、(﹣a,﹣2b) B、(﹣2a,﹣b) C、(﹣2b,﹣2a) D、(﹣2a,﹣2b)7. 如图,已知四边形ABCD是平行四边形,从下列条件:①AB=BC,②∠ABC=90°,
A、(﹣a,﹣2b) B、(﹣2a,﹣b) C、(﹣2b,﹣2a) D、(﹣2a,﹣2b)7. 如图,已知四边形ABCD是平行四边形,从下列条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中,再选两个做为补充,使▱ABCD变为正方形.下面四种组
合,错误的是( )
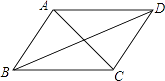 A、①② B、①③ C、②③ D、②④8. 函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A、①② B、①③ C、②③ D、②④8. 函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A、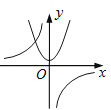 B、
B、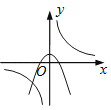 C、
C、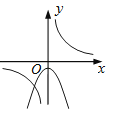 D、
D、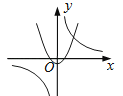
二、填空题
-
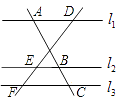
9. cos45°﹣sin30°tan60°= .10. 把抛物线y=﹣2x2的图象先向上平移3个单位,再向右平移1个单位,则平移后抛物线的解析式为 .11. 某企业前年缴税30万元,今年缴税36.3万元.那么该企业缴税的平均增长率为 .12. 如图,l1∥l2∥l3 , 两条直线与这三条平行线分别交于点A,B,C和D,E,F.
若AB=4,BC=3,DE=6,则DF= .
 13. 如图,在▱ABCD中,AM= AD,BD与MC相交于点O,则S△MOD:S△COD= .
13. 如图,在▱ABCD中,AM= AD,BD与MC相交于点O,则S△MOD:S△COD= . 14. 已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,则关于x的一元一次方程ax2+bx+c=2(a≠0)的解为 .
14. 已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,则关于x的一元一次方程ax2+bx+c=2(a≠0)的解为 .
三、作图题
-
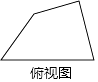
15. 已知某四棱柱的俯视图如图所示,画出它的主视图和左视图.
 16. 解答题。(1)、解方程:x2﹣2x﹣3=0(2)、若关于x的方程2x2﹣5x+c=0没有实数根,求c的取值范围.
16. 解答题。(1)、解方程:x2﹣2x﹣3=0(2)、若关于x的方程2x2﹣5x+c=0没有实数根,求c的取值范围.四、四.解答题
-
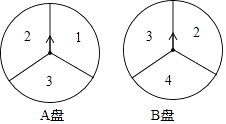
17. 小明和小亮用如图所示的两个转盘(每个转盘被分成三个面积相等的扇形)做游戏,转动两个转盘各一次,若两次数字之和为奇数,则小明胜;若两次数字之和为偶数,则小亮胜,这个游戏对双方公平吗?说说你的理由.
 18. 我们知道,蓄电池的电压为定值,使用此电源时,用电器的电流I(A)与电阻R(Ω)成反比例.已知电阻R=7.5Ω时,电流I=2A.(1)、求确定I与R之间的函数关系式并说明此蓄电池的电压是多少;(2)、若以此蓄电池为电源的用电器额定电流不能超过5A,则该电路中电阻的电阻值应满足什么条件?19. 小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(计算结果精确到1m)
18. 我们知道,蓄电池的电压为定值,使用此电源时,用电器的电流I(A)与电阻R(Ω)成反比例.已知电阻R=7.5Ω时,电流I=2A.(1)、求确定I与R之间的函数关系式并说明此蓄电池的电压是多少;(2)、若以此蓄电池为电源的用电器额定电流不能超过5A,则该电路中电阻的电阻值应满足什么条件?19. 小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(计算结果精确到1m)(参考数据:sin15°= ,cos15°= ,tan15°= )
 20. 如图,隧道的截面由抛物线和长方形构成.长方形的长为12m,宽为5m,抛物线的最高点C离路面AA1的距离为8m,建立如图所示的直角坐标系.
20. 如图,隧道的截面由抛物线和长方形构成.长方形的长为12m,宽为5m,抛物线的最高点C离路面AA1的距离为8m,建立如图所示的直角坐标系.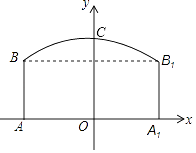 (1)、求该抛物线的函数表达式,并求出自变量x的取值范围;(2)、一大型货运汽车装载大型设备后高为6m,宽为4m.如果该隧道内设双向行车道,那么这辆货车能否安全通过?21. 已知:如图,▱ABCD的两条对角线相交于点O,E是BO的中点.过点B作AC的平行线BF,交CE的延长线于点F,连接AF.
(1)、求该抛物线的函数表达式,并求出自变量x的取值范围;(2)、一大型货运汽车装载大型设备后高为6m,宽为4m.如果该隧道内设双向行车道,那么这辆货车能否安全通过?21. 已知:如图,▱ABCD的两条对角线相交于点O,E是BO的中点.过点B作AC的平行线BF,交CE的延长线于点F,连接AF. (1)、求证:△FBE≌△COE;(2)、将▱ABCD添加一个条件,使四边形AFBO是菱形,并说明理由.22. 服装厂生产某品牌的T恤衫,每件成本是10元,根据调查,服装厂以批发单价13元给经销商,经销商愿意经销1000件,并且表示每件降价0.1元,愿意多经销100件,所以服装厂打算即不亏本,又要低于13元的单价批发给经销商.(1)、求服装厂获得利润y(元)与批发单价x(元)之间的函数关系式,并写出自变量x的取值范围;(2)、服装厂批发单价是多少时可以获得最大利润?最大利润是多少?23. 问题提出:如图(1),在边长为a(a>2)的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求S正方形MNPQ .
(1)、求证:△FBE≌△COE;(2)、将▱ABCD添加一个条件,使四边形AFBO是菱形,并说明理由.22. 服装厂生产某品牌的T恤衫,每件成本是10元,根据调查,服装厂以批发单价13元给经销商,经销商愿意经销1000件,并且表示每件降价0.1元,愿意多经销100件,所以服装厂打算即不亏本,又要低于13元的单价批发给经销商.(1)、求服装厂获得利润y(元)与批发单价x(元)之间的函数关系式,并写出自变量x的取值范围;(2)、服装厂批发单价是多少时可以获得最大利润?最大利润是多少?23. 问题提出:如图(1),在边长为a(a>2)的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求S正方形MNPQ .问题探究:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图(2)).
 (1)、若将上述四个等腰三角形拼成一个新的正方形(无缝隙,不重叠),则新正方形的边长为;这个新正方形与原正方形ABCD的面积有何关系;(填“>”,“=”“或<”);通过上述的分析,可以发现S正方形MNPQ与S△FSB之间的关系是:(2)、问题解决:求S正方形MNPQ .(3)、拓展应用:如图(3),在等边△ABC各边上分别截取AD=BE=CF=1,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△PQR,求S△PQR .
(1)、若将上述四个等腰三角形拼成一个新的正方形(无缝隙,不重叠),则新正方形的边长为;这个新正方形与原正方形ABCD的面积有何关系;(填“>”,“=”“或<”);通过上述的分析,可以发现S正方形MNPQ与S△FSB之间的关系是:(2)、问题解决:求S正方形MNPQ .(3)、拓展应用:如图(3),在等边△ABC各边上分别截取AD=BE=CF=1,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△PQR,求S△PQR .(请仿照上述探究的方法,在图3的基础上,先画出图形,再解决问题).
24.如图,在△ABC中,AB=AC=10cm,BC=12cm,点P从点C出发,在线段CB上以每秒1cm的速度向点B匀速运动.与此同时,点M从点B出发,在线段BA上以每秒lcm的速度向点A匀速运动.过点P作PN⊥BC,交AC点N,连接MP,MN.当点P到达BC中点时,点P与M同时停止运动.设运动时间为t秒(t>0).
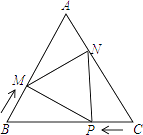 (1)、当t为何值时,PM⊥AB.(2)、设△PMN的面积为y(cm2),求出y与x之间的函致关系式.(3)、是否存在某一时刻t,使S△PMN:S△ABC=1:5?若存在,求出t的值;若不存在,说明理由.
(1)、当t为何值时,PM⊥AB.(2)、设△PMN的面积为y(cm2),求出y与x之间的函致关系式.(3)、是否存在某一时刻t,使S△PMN:S△ABC=1:5?若存在,求出t的值;若不存在,说明理由.