2016-2017学年江苏省扬州市邗江区九年级上学期期末数学试卷

试卷更新日期：2017-03-13 类型：期末考试

进入出卷网下载

一、选择题

1. 从单词“hello”中随机抽取一个字母，抽中l的概率为（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
2. 一元二次方程x²+x﹣3=0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
3. 若x₁ ， x₂是一元二次方程2x²﹣x﹣3=0的两根，则x₁+x₂的值是（）

A、﹣1 B、2 C、 $\frac{1}{2}$ D、3

查看试题解析
4.
如图，在宽为20米，长为32米的矩形地面上修筑同样宽的道路（图中阴影部分），余下部分种植草坪，要使草坪的面积为540平方米，设道路的宽为x米，则下列方程正确的是（）

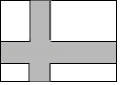A、32×20﹣20x﹣30x=540 B、32×20﹣20x﹣30x﹣x²=540 C、（32﹣x）（20﹣x）=540 D、32×20﹣20x﹣30x+2x²=540

查看试题解析
5. 下列说法中，正确的是（）

A、三点确定一个圆 B、三角形有且只有一个外接圆 C、四边形都有一个外接圆 D、圆有且只有一个内接三角形

查看试题解析
6. 已知二次函数y=ax²+bx+c中，函数y与自变量x的部分对应值如表，则方程ax²+bx+c=0的一个解的范围是（）
x
6.17
6.18
6.19
6.20
y
﹣0.03
﹣0.01
0.02
0.04

A、﹣0.01＜x＜0.02 B、6.17＜x＜6.18 C、6.18＜x＜6.19 D、6.19＜x＜6.20

查看试题解析
7. 如图，点E在y轴上，⊙E与x轴交于点A、B，与y轴交于点C、D，若C（0，16），D（0，﹣4），则线段AB的长度为（）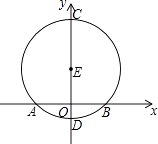

A、10 B、8 C、20 D、16

查看试题解析
8.
如图，分别过点P_i（i，0）（i=1、2、…、n）作x轴的垂线，交 $y = \frac{1}{2} x^{2}$ 的图象于点A_i ，交直线 $y = - \frac{1}{2} x$ 于点B_i ．则 $\frac{1}{A_{1} B_{1}} + \frac{1}{A_{2} B_{2}} + \dots + \frac{1}{A_{n} B_{n}}$ 的值为（）

A、 $\frac{2 n}{n + 1}$ B、2 C、 $\frac{2}{n (n + 1)}$ D、 $\frac{2}{n + 1}$

查看试题解析

二、填空题

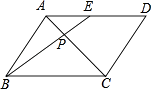
9. 已知关于x的一元二次方程x²﹣2x+k=0的一个根是3，则另一个根是．

查看试题解析
10. 二次函数y=x²+5的图象的顶点坐标为．

查看试题解析
11. 如图，点E是▱ABCD的边AD的中点，BE与AC相交于点P，则S_△_APE：S_△_BCP= ．

查看试题解析
12. 弧的半径为24，所对圆心角为60°，则弧长为．

查看试题解析
13. 近年来，我国持续大面积的雾霾天气让环保和健康问题成为焦点，为进一步普及环保和健康知识，我市某校举行了“建设宜居扬州，关注环境保护”的知识竞赛，某班学生的成绩统计如下：
成绩（分）
60
70
80
90
100
人数
4
8
12
11
5
则该班学生成绩的中位数是．

查看试题解析
14. 如图，AB是⊙O的直径，C、D是⊙O上的点，∠CDB=20°，过点C作⊙O的切线交AB的延长线于点E，则∠E= ．

查看试题解析
15. 如图，△ABC中，AE交BC于点D，∠CAE=∠CBE，AD：DE=3：5，AE=16，BD=8，则DC的长等于．

查看试题解析
16. 如图，AB是⊙O的弦，AB=10，点C是⊙O上的一个动点，且∠ACB=45°，若点M，N分别是AB、BC的中点，则MN长的最大值是．

查看试题解析
17. 某菜农搭建了一个横截面为抛物线的大棚，尺寸如图，若菜农身高为1.8m，他在不弯腰的情况下，在棚内的横向活动范围是 m．

查看试题解析
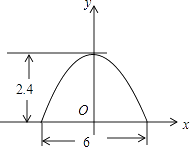18. 在平面直角坐标系中，点O为坐标原点，A、B、C三点的坐标为（ $\sqrt{3}$ ，0）、（3 $\sqrt{3}$ ，0）、（0，5），点D在第一象限，且∠ADB=60°，则线段CD的长的最小值为．

查看试题解析

三、解答题

19. 解下列方程：

(1)、x（x+4）=﹣3（x+4）；

(2)、（2x+1）（x﹣3）=﹣6．

查看试题解析
20. 射击队为从甲、乙两名运动员中选拔一人参加比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
第一次
第二次
第三次
第四次
第五次
第六次
平均成绩
中位数
甲
10
8
9
8
10
9
9

乙
10
7
10
10
9
8

9.5

(1)、完成表中填空①；②；

(2)、请计算甲六次测试成绩的方差；

(3)、若乙六次测试成绩方差为 $\frac{4}{3}$ ，你认为推荐谁参加比赛更合适，请说明理由．

查看试题解析
21. 如图，A，B两个转盘分别被平均分成三个、四个扇形，分别转动A盘、B盘各一次．转动过程中，指针保持不动，如果指针恰好指在分割线上，则重转一次，直到指针指向一个数字所在的区域为止．请用列表或画树状图的方法，求两个转盘停止后指针所指区域内的数字之积小于6的概率．

查看试题解析
22. 已知：关于x的一元二次方程x²﹣6x﹣m=0有两个实数根．

(1)、求m的取值范围；

(2)、如果m取符合条件的最小整数，且一元二次方程x²﹣6x﹣m=0与x²+nx+1=0有一个相同的根，求常数n的值．

查看试题解析
23. 扬州一农场去年种植水稻10亩，总产量为6000kg，今年该农场扩大了种植面积，并且引进新品种“超级水稻”，使总产量增加到18000kg，已知种植面积的增长率是平均亩产量的增长率的2倍，求平均亩产量的增长率．

查看试题解析
24. 如图，△ABC中，D是BC上一点，∠DAC=∠B，E为AB上一点．

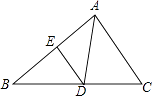(1)、求证：△CAD∽△CBA；

(2)、若BD=10，DC=8，求AC的长；

(3)、在（2）的条件下，若DE∥AC，AE=4，求BE的长．

查看试题解析
25. 如图，Rt△ABC，∠C=90°，点D为AB上的一点，以AD为直径的⊙O与BC相切于点E，连接AE．

(1)、求证：AE平分∠BAC；

(2)、若AC=8，OB=18，求BD的长．

查看试题解析
26. 某鲜花销售部在春节前20天内销售一批鲜花．其中，该销售部公司的鲜花批发部日销售量y₁（万朵）与时间x（x为整数，单位：天）关系为二次函数，部分对应值如表所示．
时间x（天）
0
4
8
12
16
20
销量y₁（万朵）
0
16
24
24
16
0
与此同时，该销售部还通过某网络电子商务平台销售鲜花，网上销售日销售量y₂（万朵）与时间x（x为整数，单位：天）的函数关系如图所示．

(1)、求y₁与x的二次函数关系式及自变量x的取值范围；

(2)、求y₂与x的函数关系式及自变量x的取值范围；

(3)、当8≤x≤20时，设该花木公司鲜花日销售总量为y万朵，写出y与时间x的函数关系式，并判断第几天日销售总量y最大，并求出此时的最大值．

查看试题解析
27. 如图，正方形ABCD的边长为4，点G，H分别是BC、CD边上的点，直线GH与AB、AD的延长线相交于点E，F，连接AG、AH．

(1)、当BG=2，DH=3时，则GH：HF= ， ∠AGH=°；

(2)、若BG=3，DH=1，求DF、EG的长；

(3)、设BG=x，DH=y，若△ABG∽△FDH，求y与x之间的函数关系式，并求出y的取值范围．

查看试题解析
28. 如图，二次函数y=x²﹣4x的图象与x轴、直线y=x的一个交点分别为点A，B，CD是线段OB上的一动线段，且CD=2，过点C，D的两直线都平行于y轴，与抛物线相交于点F，E，连接EF．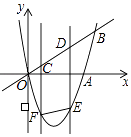

(1)、点A的坐标为，线段OB的长=；

(2)、设点C的横坐标为m
①当四边形CDEF是平行四边形时，求m的值；
②连接AC、AD，求m为何值时，△ACD的周长最小，并求出这个最小值．

查看试题解析

	第一次	第二次	第三次	第四次	第五次	第六次	平均成绩	中位数
甲	10	8	9	8	10	9	9
乙	10	7	10	10	9	8		9.5

x	6.17	6.18	6.19	6.20
y	﹣0.03	﹣0.01	0.02	0.04

成绩（分）	60	70	80	90	100
人数	4	8	12	11	5

时间x（天）	0	4	8	12	16	20
销量y₁（万朵）	0	16	24	24	16	0