2016-2017学年四川省成都市金牛区八年级上学期期末数学试卷
试卷更新日期:2017-03-13 类型:期末考试
一、选择题
-
1. 4的平方根是( )A、±2 B、﹣2 C、2 D、162. 实数π, ,﹣3. , , 中,无理数有( )个.A、1 B、2 C、3 D、43. 要使式子 有意义,则x的取值范围是( )A、x>2 B、x>﹣2 C、x≥2 D、x≥﹣24. 下列各组数中不能作为直角三角形三边长的是( )A、 , , B、7,24,25 C、6,8,10 D、1,2,35.
如图所示,点A(﹣1,m),B(3,n)在一次函数y=kx+b的图象上,则( )
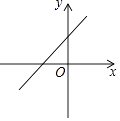 A、m=n B、m>n C、m<n D、m、n的大小关系不确定6. 下列命题为真命题的是( )A、若a2=b2 , 则a=b B、等角的余角相等 C、同旁内角相等,两直线平行 D、 = ,SA2>SB2 , 则A组数据更稳定7.
A、m=n B、m>n C、m<n D、m、n的大小关系不确定6. 下列命题为真命题的是( )A、若a2=b2 , 则a=b B、等角的余角相等 C、同旁内角相等,两直线平行 D、 = ,SA2>SB2 , 则A组数据更稳定7.抢微信红包成为节日期间人们最喜欢的活动之一.对某单位50名员工在春节期间所抢的红包金额进行统计,并绘制成了统计图.根据如图提供的信息,红包金额的众数和中位数分别是( )
 A、20,20 B、30,20 C、30,30 D、20,308. 如图所示,直线y=kx+b(k≠0)与x轴交于点(﹣5,0),则关于x的方程kx+b=0的解为x=( )
A、20,20 B、30,20 C、30,30 D、20,308. 如图所示,直线y=kx+b(k≠0)与x轴交于点(﹣5,0),则关于x的方程kx+b=0的解为x=( ) A、﹣5 B、﹣4 C、0 D、19. 下列各曲线表示的y与x的关系中,y不是x的函数的是( )A、
A、﹣5 B、﹣4 C、0 D、19. 下列各曲线表示的y与x的关系中,y不是x的函数的是( )A、 B、
B、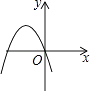 C、
C、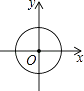 D、
D、 10. 园林队在某公园进行绿化,中间休息了一段时间,绿化面积S(单位:平方米)与工作时间t(单位:小时)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为( )
10. 园林队在某公园进行绿化,中间休息了一段时间,绿化面积S(单位:平方米)与工作时间t(单位:小时)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为( ) A、40平方米 B、50平方米 C、65平方米 D、80平方米
A、40平方米 B、50平方米 C、65平方米 D、80平方米二、填空题
-
11. 若x,y为实数,且满足|x﹣3|+ =0,则( )2017的值是 .12. 在平面直角坐标系内,一个点的坐标为(2,﹣3),则它关于x轴对称的点的坐标是 .13. 如图,已知一次函数y1=k1x+b1和y2=k2x+b2的图象交于点P(2,4),则关于x的方程k1x+b1=k2x+b2的解是 .
 14. 如图,已知AE∥BD,∠1=130°,∠2=30°,则∠C= .
14. 如图,已知AE∥BD,∠1=130°,∠2=30°,则∠C= .
三、解答题
-
15. 计算下列各题(1)、 +|1﹣ |+( )﹣1﹣20170(2)、 × ﹣( ﹣1)2 .16. 解方程(不等式)组(1)、解方程组:(2)、解不等式组: ,并把解集在数轴上表示出来.
 17. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.∠1=∠2,∠3=105°,求∠ACB的度数.
17. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.∠1=∠2,∠3=105°,求∠ACB的度数.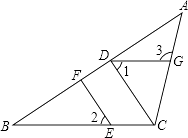 18. 某校为了进一步改进本校八年级数学教学,提高学生学习数学的兴趣,校教务处在八年级所有班级中,每班随机抽取了部分学生,并对他们的数学学习情况进行了问卷调查.我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A﹣非常喜欢“、“B﹣比较喜欢“、“C﹣不太喜欢“、“D﹣很不喜欢“,针对这个题目,问卷时要求被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下两幅不完整的统计图.
18. 某校为了进一步改进本校八年级数学教学,提高学生学习数学的兴趣,校教务处在八年级所有班级中,每班随机抽取了部分学生,并对他们的数学学习情况进行了问卷调查.我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A﹣非常喜欢“、“B﹣比较喜欢“、“C﹣不太喜欢“、“D﹣很不喜欢“,针对这个题目,问卷时要求被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下两幅不完整的统计图.
请你根据以上提供的信息,解答下列问题:
(1)、补全上面的条形统计图和扇形统计图;(2)、所抽取学生对数学学习喜欢程度的众数是;(3)、若该校八年级共有1000名学生,请你估计该年级学生对数学学习“不太喜欢”的有多少人?19. 已知:用2辆A型车和1辆B型车载满货物一次可运货10吨; 用1辆A型车和2辆B型车载满货物一次可运货11吨.根据以上信息,解答下列问题:(1)、1辆A型车和1辆B型车载满货物一次可分别运货多少吨?(2)、某物流公司现有货物若干吨要运输,计划同时租用A型车6辆,B型车8辆,一次运完,且恰好每辆车都满载货物,请求出该物流公司有多少吨货物要运输?20. 在平面直角坐标系xOy中,一次函数的图象经过点A(4,1)与点B(0,5). (1)、求一次函数的表达式;(2)、若P点为此一次函数图象上一点,且S△POB= S△AOB , 求P点的坐标.21. 已知0≤x≤3,化简 = .22. 如图,圆柱体的高为12cm,底面周长为10cm,圆柱下底面A点除有一只蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是 cm.
(1)、求一次函数的表达式;(2)、若P点为此一次函数图象上一点,且S△POB= S△AOB , 求P点的坐标.21. 已知0≤x≤3,化简 = .22. 如图,圆柱体的高为12cm,底面周长为10cm,圆柱下底面A点除有一只蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是 cm.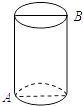 23. 如图,直线y=﹣x+m与y=nx+5n(n≠0)的交点横坐标为﹣3,则关于的不等式﹣x+m>nx+5n>0的整数解是 .
23. 如图,直线y=﹣x+m与y=nx+5n(n≠0)的交点横坐标为﹣3,则关于的不等式﹣x+m>nx+5n>0的整数解是 . 24. 如图,点P的坐标为(2,0),点B在直线y=x+m上运动,当线段PB最短时,PB的长度是 .
24. 如图,点P的坐标为(2,0),点B在直线y=x+m上运动,当线段PB最短时,PB的长度是 .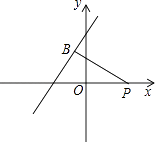 25. 如图,平面直角坐标系中,已知直线y=x上一点P(2,2),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,连接CD,直线CD与直线y=x交于点Q,当△OPC≌△ADP时,则C点的坐标是 , Q点的坐标是 .
25. 如图,平面直角坐标系中,已知直线y=x上一点P(2,2),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,连接CD,直线CD与直线y=x交于点Q,当△OPC≌△ADP时,则C点的坐标是 , Q点的坐标是 .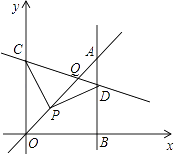
四、解答题
-
26. 春天来了,小明骑自行车从家里出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
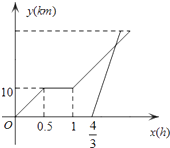 (1)、直接写出小明开始骑车的0.5小时内所对应的函数解析式 .(2)、小明从家出发多少小时后被妈妈追上?此时离家多远?(3)、若妈妈比小明早12分钟到达乙地,求从家到乙地的路程.27. 通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整.
(1)、直接写出小明开始骑车的0.5小时内所对应的函数解析式 .(2)、小明从家出发多少小时后被妈妈追上?此时离家多远?(3)、若妈妈比小明早12分钟到达乙地,求从家到乙地的路程.27. 通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整.
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连结EF,试猜想EF、BE、DF之间的数量关系.
(1)、思路梳理把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,由∠ADG=∠B=90°,得∠FDG=180°,即点F、D、G共线,易证△AFG≌ , 故EF、BE、DF之间的数量关系
为 .
(2)、类比引申如图2,点E、F分别在正方形ABCD的边CB、DC的延长线上,∠EAF=45°,连结EF,试猜想EF、BE、DF之间的数量关系为 , 并给出证明.
(3)、联想拓展如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠BAD+∠EAC=45°,若BD=3,EC=6,求DE的长.
28.如图1,在平面直角坐标系中,点A坐标为(﹣4,4),点B的坐标为(4,0).
 (1)、求直线AB的解析式;(2)、点M是坐标轴上的一个点,若AB为直角边构造直角三角形△ABM,请求出满足条件的所有点M的坐标;(3)、如图2,以点A为直角顶点作∠CAD=90°,射线AC交x轴的负半轴与点C,射线AD交y轴的负半轴与点D,当∠CAD绕点A旋转时,OC﹣OD的值是否发生变化?若不变,直接写出它的值;若变化,直接写出它的变化范围(不要解题过程).
(1)、求直线AB的解析式;(2)、点M是坐标轴上的一个点,若AB为直角边构造直角三角形△ABM,请求出满足条件的所有点M的坐标;(3)、如图2,以点A为直角顶点作∠CAD=90°,射线AC交x轴的负半轴与点C,射线AD交y轴的负半轴与点D,当∠CAD绕点A旋转时,OC﹣OD的值是否发生变化?若不变,直接写出它的值;若变化,直接写出它的变化范围(不要解题过程).