2016-2017学年江苏省盐城市建湖县九年级上学期期末数学试卷
试卷更新日期:2017-03-13 类型:期末考试
一、选择题:
-
1. 抛物线y=2(x﹣3)2﹣1的顶点坐标是( )A、(3,1) B、(3,﹣1) C、(﹣3,1) D、(﹣3,﹣1)2. 在Rt△ABC中,∠C=90°,a=4,b=3,则cosA的值是( )A、 B、 C、 D、3. 初三体育素质测试,某小组5名同学成绩如下表所示,有两个数据被遮盖,如下表:那么被遮盖的两个数据依次是( )
编号
1
2
3
4
5
方差
平均成绩
得分
38
34
■
37
40
■
37
A、35,2 B、36,4 C、35,3 D、36,54. 如图,已知a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F,若 = ,则 的值是( )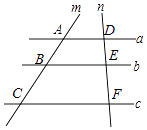 A、 B、 C、 D、15. 如图,△ACD和△ABC相似需具备的条件是( )
A、 B、 C、 D、15. 如图,△ACD和△ABC相似需具备的条件是( )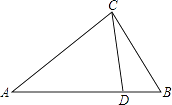 A、 B、 C、AC2=AD•AB D、CD2=AD•BD6. 在同一时刻太阳光线是平行的,如果高1.5米的测杆影长3米,那么此时影长36米的旗杆的高度为( )A、18米 B、12米 C、15米 D、20米7. 已知抛物线y=x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( )
A、 B、 C、AC2=AD•AB D、CD2=AD•BD6. 在同一时刻太阳光线是平行的,如果高1.5米的测杆影长3米,那么此时影长36米的旗杆的高度为( )A、18米 B、12米 C、15米 D、20米7. 已知抛物线y=x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( )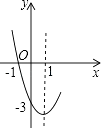 A、﹣1<x<4 B、x<﹣1或x>3 C、x<﹣1或x>4 D、﹣1<x<38. 如图,边长分别为2和4的两个全等三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止,设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )
A、﹣1<x<4 B、x<﹣1或x>3 C、x<﹣1或x>4 D、﹣1<x<38. 如图,边长分别为2和4的两个全等三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止,设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( ) A、
A、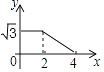 B、
B、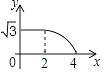 C、
C、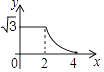 D、
D、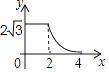
二、填空题:
-
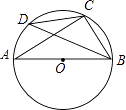
9. 如果 ,那么 = .10. 抛物线y=2x2﹣bx+3的对称轴是直线x=﹣2,则b的值为 .11. 一元二次方程x(x﹣2)=0的解是 .12. 如图,AB是⊙O的直径,点C,D都在⊙O上,∠ABC=50°,则∠BDC的大小是 .
 13. 已知两相似三角形对应高的比为3:10,且这两个三角形的周长差为56cm,则较小的三角形的周长为 .14.
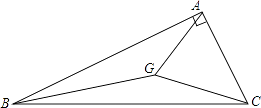
13. 已知两相似三角形对应高的比为3:10,且这两个三角形的周长差为56cm,则较小的三角形的周长为 .14.如图,△ABC中,∠BAC=90°,点G是△ABC的重心,如果AG=4,那么BC的长为 .
 15. 如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP= .
15. 如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP= . 16. 一位运动员投掷铅球,如果铅球运行时离地面的高度为y(米)关于水平距离x(米)的函数解析式为y=﹣ x2+ x+ ,那么铅球运动过程中最高点离地面的距离为米.17. 如图,在平面直角坐标系中,点A(﹣3,﹣1)、B(﹣2,﹣4)、C(﹣6,﹣5),以原点位似中心将△ABC缩小,位似比为1:2,则点B的对应点的坐标为 .
16. 一位运动员投掷铅球,如果铅球运行时离地面的高度为y(米)关于水平距离x(米)的函数解析式为y=﹣ x2+ x+ ,那么铅球运动过程中最高点离地面的距离为米.17. 如图,在平面直角坐标系中,点A(﹣3,﹣1)、B(﹣2,﹣4)、C(﹣6,﹣5),以原点位似中心将△ABC缩小,位似比为1:2,则点B的对应点的坐标为 .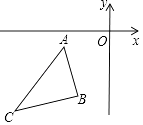 18. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论是 . (写出正确命题的序号)
18. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论是 . (写出正确命题的序号)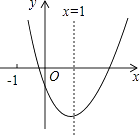
三、解答题:
-
19. 计算:﹣ tan60°+4sin30°×cos245°.20. 一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,记录颜色后放回,搅匀,再从中任意摸出1个球.(1)、请用画树状图或列表的方法列出所有可能出现的结果;(2)、求两次摸到“一只白球、一只红球”的概率.21. △ABC中,∠A=30°,∠B=45°,AC=4,求AB的长?
 22. 已知二次函数y=x2+bx+c的图象与直线y=x+1相交于点A(﹣1,m)和点B(n,5).
22. 已知二次函数y=x2+bx+c的图象与直线y=x+1相交于点A(﹣1,m)和点B(n,5). (1)、求该二次函数的关系式;(2)、在给定的平面直角坐标系中,画出这两个函数的大致图象;(3)、结合图象直接写出x2+bx+c>x+1时x的取值范围.23. 已知二次函数y=x2﹣(2m+1)+( m2﹣1).(1)、求证:不论m取什么实数,该二次函数图象与x轴总有两个交点;(2)、若该二次函数图象经过点(2m﹣2,﹣2m﹣1),求该二次函数的表达式.24. 如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且 = = .
(1)、求该二次函数的关系式;(2)、在给定的平面直角坐标系中,画出这两个函数的大致图象;(3)、结合图象直接写出x2+bx+c>x+1时x的取值范围.23. 已知二次函数y=x2﹣(2m+1)+( m2﹣1).(1)、求证:不论m取什么实数,该二次函数图象与x轴总有两个交点;(2)、若该二次函数图象经过点(2m﹣2,﹣2m﹣1),求该二次函数的表达式.24. 如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且 = = .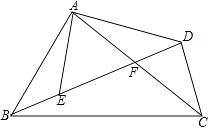 (1)、试问:∠BAE与∠CAD相等吗?为什么?(2)、试判断△ABE与△ACD是否相似?并说明理由.25. 如图,操场上有一根旗杆AH,为测量它的高度,在B和D处各立一根高1.5米的标杆BC、DE,两杆相距30米,测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H,B,F,D,G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?
(1)、试问:∠BAE与∠CAD相等吗?为什么?(2)、试判断△ABE与△ACD是否相似?并说明理由.25. 如图,操场上有一根旗杆AH,为测量它的高度,在B和D处各立一根高1.5米的标杆BC、DE,两杆相距30米,测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H,B,F,D,G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?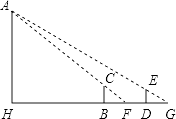 26. 某网店以每件40元的价格购进一款童装,由试销知,每星期的销售量t(件)与每件的销售价x(元)之间的函数关系式为t=30x+2100.(1)、求每星期销售这款童装的毛利润y(元)与每件销售价x(元)之间的函数表达式;(2)、当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?(3)、为了使每星期利润不少于6000元,求每件销售价x的取值范围.27. 如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点D,交AB的延长线于点E,连接CD、CE.
26. 某网店以每件40元的价格购进一款童装,由试销知,每星期的销售量t(件)与每件的销售价x(元)之间的函数关系式为t=30x+2100.(1)、求每星期销售这款童装的毛利润y(元)与每件销售价x(元)之间的函数表达式;(2)、当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?(3)、为了使每星期利润不少于6000元,求每件销售价x的取值范围.27. 如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点D,交AB的延长线于点E,连接CD、CE. (1)、求证:△ACD∽△AEC;(2)、当 = 时,求tanE;(3)、若AD=4,AC=4 ,求△ACE的面积.28. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,且抛物线经过A(﹣1,0),C(0,﹣5)两点,与x轴交于点B.
(1)、求证:△ACD∽△AEC;(2)、当 = 时,求tanE;(3)、若AD=4,AC=4 ,求△ACE的面积.28. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,且抛物线经过A(﹣1,0),C(0,﹣5)两点,与x轴交于点B.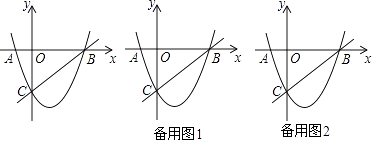 (1)、若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;(2)、设点P为抛物线上的一个动点,连接PB、PC,若△BPC是以BC为直角边的直角三角形,求此时点P的坐标;(3)、在抛物线上BC段有另一个动点Q,以点Q为圆心作⊙Q,使得⊙Q与直线BC相切,在运动的过程中是否存在一个最大⊙Q?若存在,请直接写出最大⊙Q的半径;若不存在,请说明理由.
(1)、若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;(2)、设点P为抛物线上的一个动点,连接PB、PC,若△BPC是以BC为直角边的直角三角形,求此时点P的坐标;(3)、在抛物线上BC段有另一个动点Q,以点Q为圆心作⊙Q,使得⊙Q与直线BC相切,在运动的过程中是否存在一个最大⊙Q?若存在,请直接写出最大⊙Q的半径;若不存在,请说明理由.