2016-2017学年山东省泰安市肥城市八年级上学期期末数学试卷

试卷更新日期：2017-03-13 类型：期末考试

进入出卷网下载

一、选择题

1. 下列图案中，轴对称图形的个数是（）

A、3 B、2 C、1 D、0

查看试题解析
2. 下列命题是真命题的是（）

A、两个锐角的和一定是钝角 B、两条平行线被第三条直线所截，同旁内角的平分线互相垂直 C、两条直线被第三条直线所截，同旁内角互补 D、直线外一点到这条直线的垂线段，叫做这点到该直线的距离

查看试题解析
3. 某商场一天中售出李宁牌运动鞋11双，其中各种尺码的鞋的销售量如下表所示，
鞋的尺码（单位：厘米）
23.5
24
24.5
25
26
销售量（单位：双）
1
2
2
5
1
则这11双鞋的尺码组成一组数据中众数和中位数分别为（）

A、25，25 B、24.5，25 C、26，25 D、25，24.5

查看试题解析
4.
如图，已知∠1=∠2，AC=AD，增加下列条件：①AB=AE；②BC=ED；③∠C=∠D；④∠B=∠E．其中能使△ABC≌△AED的条件有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
5. 如图所示，已知AB∥CD，∠A=50°，∠C=∠E．则∠C等于（）

A、20° B、25° C、30° D、40°

查看试题解析
6. 分式方程 $\frac{x}{x - 2} - \frac{1}{x^{2} - 4} = 1$ 的解是（）

A、﹣ $\frac{3}{2}$ B、﹣2 C、﹣ $\frac{5}{2}$ D、 $\frac{3}{2}$

查看试题解析
7. 如图，△ABC中，以B为圆心，BC长为半径画弧，分别交AC，AB于D，E两点，并连接BD，DE．若∠A=30°，AB=AC，则∠BDE的度数为何（）

A、45 B、52.5 C、67.5 D、75

查看试题解析
8. 如图，△ABC中，∠A=36°，AB=AC，BD平分∠ABC，DE∥BC，则图中等腰三角形的个数（）

A、1个 B、3个 C、4个 D、5个

查看试题解析
9. 如图，把矩形纸片ABCD纸沿对角线折叠，设重叠部分为△EBD，那么下列说法错误的是（）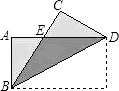

A、△EBD是等腰三角形，EB=ED B、折叠后∠ABE和∠CBD一定相等 C、折叠后得到的图形是轴对称图形 D、△EBA和△EDC一定是全等三角形

查看试题解析
10. 如图，△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于F，若BF=AC，则∠ABC的大小是（）

A、40° B、45° C、50° D、60°

查看试题解析
11. 如图，△ABC中边AB的垂直平分线分别交BC，AB于点D，E，AE=3cm，△ADC的周长为9cm，则△ABC的周长是（）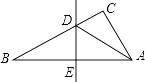

A、10cm B、12cm C、15cm D、17cm

查看试题解析
12. 如图，在Rt△ABC中，∠B=90°，ED是AC的垂直平分线，交AC于点D，交BC于点E．已知∠BAE=10°，则∠C的度数为（）

A、30° B、40° C、50° D、60°

查看试题解析
13. 甲、乙两班举行电脑汉字输入比赛，参赛学生每分钟输入汉字的个数统计结果如下表：
班级
参赛人数
中位数
方差
平均数
甲
55
149
191
135
乙
55
151
110
135
某同学分析上表后得出如下结论：
①甲、乙两班学生成绩平均水平相同；
②乙班优秀的人数多于甲班优秀的人数（每分钟输入汉字≥150个为优秀）；
③甲班成绩的波动比乙班大，
上述结论正确的是（）

A、①②③ B、①② C、①③ D、②③

查看试题解析
14. 如图所示，△ABP与△CDP是两个全等的等边三角形，且PA⊥PD，有下列四个结论：①∠PBC=15°，②AD∥BC，③PC⊥AB，④四边形ABCD是轴对称图形，其中正确的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
15. 某厂接到加工720件衣服的订单，预计每天做48件，正好按时完成，后因客户要求提前5天交货，设每天应多做x件才能按时交货，则x应满足的方程为（）

A、 $\frac{720}{48 + x} - \frac{720}{48} = 5$ B、 $\frac{720}{48} + 5$ = $\frac{720}{48 + x}$ C、 $\frac{720}{48} - \frac{720}{x} = 5$ D、 $\frac{720}{48} - \frac{720}{48 + x} = 5$

查看试题解析

二、填空题

16. 在学校的卫生检查中，规定各班的教室卫生成绩占30%，环境卫生成绩占40%，个人卫生成绩占30%．八年级一班这三项成绩分别为85分，90分和95分，求该班卫生检查的总成绩．

查看试题解析
17. 已知 $\frac{2 b}{3 a - b}$ = $\frac{3}{4}$ ，则 $\frac{a}{b}$ = ．

查看试题解析
18.
如图，已知AB=A₁B，A₁C=A₁A₂ ， A₂D=A₂A₃ ， A₃E=A₃A₄ ， ∠B=20°，则∠A₄=度．

查看试题解析
19. 关于x的方程 $\frac{x}{x - 3}$ +1= $\frac{m}{x - 3}$ 有增根，则m的值为．

查看试题解析
20. 如图EB交AC于M，交FC于D，AB交FC于N，∠E=∠F=90°，∠B=∠C，AE=AF．给出下列结论：①∠1=∠2；②BE=CF；③△ACN≌△ABM；④CD=DN．其中正确的结论有（填序号）．

查看试题解析

三、解答题

21. 解答下列各题

(1)、解方程： $\frac{x^{2}}{4 - x^{2}}$ = $\frac{1}{x + 2} - 1$ ．

(2)、先化简，再求值： $\frac{a - 3}{3 a^{2} - 6 a} + (a + 2 - \frac{5}{a - 2})$ ，其中a²+3a﹣1=0．

查看试题解析
22. 已知，如图所示，AB=AC，BD=CD，DE⊥AB于点E，DF⊥AC于点F，求证：DE=DF．

查看试题解析
23. 市射击队为从甲、乙两名运动员中选拔一人参加省比赛，对他们进行了六次测试，测试成绩如表：

(1)、把表中所空各项数据填写完整；
选手
选拔成绩/环
中位数
平均数
甲
10
9
8
8
10
9

乙
10
10
8
10
7

9

(2)、分别计算甲、乙六次测试成绩的方差；

(3)、根据（1）、（2）计算的结果，你认为推荐谁参加省比赛更合适，请说明理由．

查看试题解析
24. 某超市用3000元购进某种干果销售，由于销售状况良好，超市又调拨9000元资金购进该种干果，但这次的进价比第一次的进价提高了20%，购进干果数量是第一次的2倍还多300千克，如果超市按每千克9元的价格出售，当大部分干果售出后，余下的600千克按售价的8折售完．

(1)、该种干果的第一次进价是每千克多少元？

(2)、超市销售这种干果共盈利多少元？

查看试题解析
25. 已知：如图①，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=50°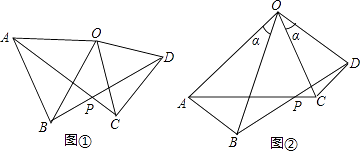

(1)、求证：①AC=BD；②∠APB=50°；

(2)、如图②，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=α，则AC与BD间的等量关系为， ∠APB的大小为

查看试题解析
26. 按要求完成下列题目．

(1)、求： $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ +…+ $\frac{1}{n (n + 1)}$ 的值．
对于这个问题，可能有的同学接触过，一般方法是考虑其中的一般项，注意到上面和式的每一项可以写成 $\frac{1}{n (n + 1)}$ 的形式，而 $\frac{1}{n (n + 1)}$ = $\frac{1}{n}$ ﹣ $\frac{1}{n + 1}$ ，这样就把 $\frac{1}{n (n + 1)}$ 一项（分）裂成了两项．
试着把上面和式的每一项都裂成两项，注意观察其中的规律，求出上面的和，并直接写出 $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ +…+ $\frac{1}{2016 \times 2017}$ 的值．

(2)、若 $\frac{1}{n (n + 1) (n + 2)}$ = $\frac{A}{n (n + 1)}$ + $\frac{B}{(n + 1) (n + 2)}$
①求：A、B的值：
②求： $\frac{1}{1 \times 2 \times 3}$ + $\frac{1}{2 \times 3 \times 4}$ +…+ $\frac{1}{n (n + 1) (n + 2)}$ 的值．

查看试题解析

鞋的尺码（单位：厘米）	23.5	24	24.5	25	26
销售量（单位：双）	1	2	2	5	1

班级	参赛人数	中位数	方差	平均数
甲	55	149	191	135
乙	55	151	110	135

选手	选拔成绩/环						中位数	平均数
甲	10	9	8	8	10	9
乙	10	10	8	10	7			9