2016-2017学年山东省青岛市李沧区八年级上学期期末数学试卷
试卷更新日期:2017-03-13 类型:期末考试
一、选择题
-
1. 9的平方根是( )A、3 B、 C、±3 D、2. 下列各数:1. 、 、 、0.020020002…(每相邻两个2之间依次多一个0)、 、 、 ,无理数有( )个.A、2 B、3 C、4 D、53. 在平面直角坐标系中,若点A(a,b)在第四象限内,则点B(a,﹣b)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列计算正确的是( )A、﹣ =﹣4 B、 =﹣3 C、 D、 =﹣45. 如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=22°,那么∠2的度数是( )
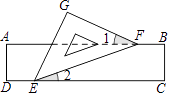 A、30° B、23° C、20° D、15°6. 已知点(﹣6,y1),(3,y2)都在直线y=﹣0.5x+5上,则y1与y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、不能比较7. 某校初三(2)班40名同学为“希望工程”捐款,共捐款100元,捐款情况如表:
A、30° B、23° C、20° D、15°6. 已知点(﹣6,y1),(3,y2)都在直线y=﹣0.5x+5上,则y1与y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、不能比较7. 某校初三(2)班40名同学为“希望工程”捐款,共捐款100元,捐款情况如表:捐款(元)
1
2
3
4
人数(人)
6
●
●
7
表格中捐款2元和3元的人数不小心被墨水污染已经看不清楚.
若设捐款2元的有x名同学,捐款3元的有y名同学,根据题意,可得方程组( )
A、 B、 C、 D、8.已知函数y=kx+b的图象如图所示,则函数y=﹣bx+k的图象大致是( )
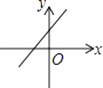 A、
A、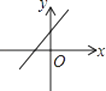 B、
B、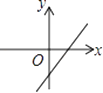 C、
C、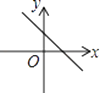 D、
D、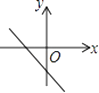
二、填空题
-
9. 的绝对值是 , 相反数是 , 倒数是 .10. 若 是方程2x﹣ay=5的一个解,则a= .11. 市运会举行射击比赛,校射击队从甲、乙、丙、丁四人中选拔一人参赛.在选拔赛中,每人射击10次,计算他们10发成绩的平均数(环)及方差如下表.请你根据表中数据选一人参加比赛,最合适的人选是 .
甲
乙
丙
丁
平均数
8.2
8.0
8.0
8.2
方差
2.1
1.8
1.6
1.4
12. 图中刀柄外形是一个直角梯形(下底挖去一小半圆),刀片上、下是平行的,转动刀片(如图)时形成∠1、∠2,则∠1+∠2=度.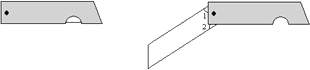 13. 如图,一个三级台阶,它的每一级的长宽和高分别为20、3、2,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是 .
13. 如图,一个三级台阶,它的每一级的长宽和高分别为20、3、2,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是 . 14.
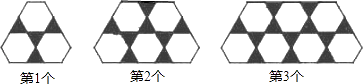
14.黑色正三角形与白色正六边形的边长相等,用它们镶嵌图案,方法如下:白色正六边形分上下两行,上面一行的正六边形个数比下面一行少一个,正六边形之间的空隙用黑色的正三角形嵌满,按第1,2,3个图案(如图)所示规律依次下去,则第n个图案中,黑色正三角形和白色正六边形的个数分别是和(用含n的代数式表示)
三、作图题
-
15. 如图,请作出△PQR关于y轴对称的△P1Q1R1 , 并写出△P1Q1R1三个顶点的坐标.

四、解答题
-
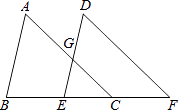
16. 计算:(1)、 × + ÷ ﹣(2)、(3+ )2﹣( +1)( ﹣1).17. 解方程组(1)、(2)、 .18. 如图,点B、E、C、F在同一直线上,AC与DE相交于点G,∠A=∠D,AC∥DF,求证:∠B=∠DEC.
 19. 6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成统计图.
19. 6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成统计图.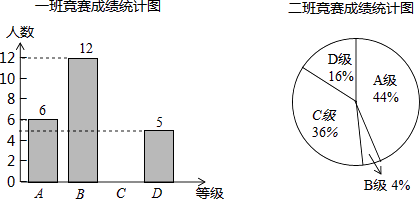
平均数(分)
中位数(分)
众数(分)
一班
a
b
90
二班
d
80
c
(1)、把一班竞赛成绩统计图补充完整;(2)、写出表中a、b、c的值:平均数(分)
中位数(分)
众数(分)
一班
a
b
90
二班
d
80
c
(3)、请从平均数和中位数方面比较一班和二班的成绩,对这次竞赛成绩的结果进行分析.20. 有一块形状为四边形的钢板,量得它的各边长度为AB=9cm,BC=12cm,CD=17cm,DA=8cm,∠B=90°.求这块钢板的面积.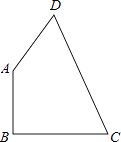 21. 某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
21. 某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.类型
价格
A型
B型
进价(元/盏)
40
65
标价(元/盏)
60
100
(1)、这两种台灯各购进多少盏?(2)、若A型台灯按标价的9折出售,B型台灯按标价的8折出售,那么这批台灯全部售出后,商场共获利多少元?22. 小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m,如图是小明和爸爸所走路程s(m)与步行时间t(min)的函数图象. (1)、图中线(填l1或l2)表示的是爸爸所走路程与步行时间的函数关系式.(2)、请分别求出l1中BC段以及l2的函数关系式.(3)、请求出小明出发多少时间与爸爸第最后一次相遇.(4)、在速度不变的情况下,小明希望比爸爸早20min到达公园,则小明在步行过程中停留的时间需作怎样的调整.23. 图形在折叠过程中会形成相等的边和相等的角,下面是同学们在数学课上所做的三角形、四边形折叠实验,请根据实验过程解决问题:
(1)、图中线(填l1或l2)表示的是爸爸所走路程与步行时间的函数关系式.(2)、请分别求出l1中BC段以及l2的函数关系式.(3)、请求出小明出发多少时间与爸爸第最后一次相遇.(4)、在速度不变的情况下,小明希望比爸爸早20min到达公园,则小明在步行过程中停留的时间需作怎样的调整.23. 图形在折叠过程中会形成相等的边和相等的角,下面是同学们在数学课上所做的三角形、四边形折叠实验,请根据实验过程解决问题: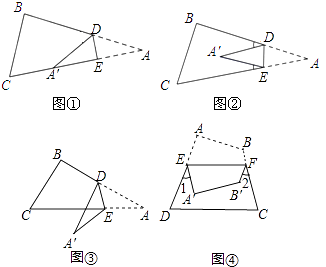
问题(一)
如图①,一张三角形ABC纸片,点D、E分别是△ABC边上两点.
(1)、如果沿直线DE折叠,使A点落在CE上,则∠BDA′和∠A的数量关系是;(2)、如果折成图②的形状,猜想∠BDA′、∠CEA′和∠A的数量关系是;(3)、如果折成图③的形状,猜想∠BDA′、∠CEA′和∠A的数量关系,并说明理由.(4)、如图④,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,∠1+∠2与∠A、∠B之间的数量关系是 . (直接写出结论)24. 如图,等腰三角形ABC中,AB=AC=5cm,BC=6cm,动点P从点A出发,沿路线A﹣B﹣C匀速运动,速度为1cm/s,运动到C点停止,设运动时间为t(s),△APC的面积为y(cm2). (1)、求△ABC的面积.(2)、求等腰△ABC腰上的高.(3)、请分别求出P在边AB(0≤t≤5)、BC(5<t≤11)上运动时,△APC的面积为y(cm2)与运动时间t(s)之间的函数关系式.(4)、是否存在某一时刻t,使得△APC的面积正好是△ABC面积的 ,若存在,求出t的值;若不存在,说明理由.(5)、当运动时间t(s)为时,(直接填空)△APC为直角三角形.
(1)、求△ABC的面积.(2)、求等腰△ABC腰上的高.(3)、请分别求出P在边AB(0≤t≤5)、BC(5<t≤11)上运动时,△APC的面积为y(cm2)与运动时间t(s)之间的函数关系式.(4)、是否存在某一时刻t,使得△APC的面积正好是△ABC面积的 ,若存在,求出t的值;若不存在,说明理由.(5)、当运动时间t(s)为时,(直接填空)△APC为直角三角形.
-