2016-2017学年山东省临沂市兰陵县八年级上学期期末数学试卷

试卷更新日期：2017-03-13 类型：期末考试

进入出卷网下载

一、选择题：

1. 下列计算，正确的是（）

A、a²•a²=2a² B、a²+a²=a⁴ C、（﹣a²）²=a⁴ D、（a+1）²=a²+1

查看试题解析
2. 多项式12ab³c+8a³b的各项公因式是（）

A、4ab² B、4abc C、2ab² D、4ab

查看试题解析
3. 下列约分正确的是（）

A、 $\frac{x + y}{x^{2} + x y}$ = $\frac{1}{x}$ B、 $\frac{x + y}{x + y}$ =0 C、 $\frac{x^{6}}{x^{2}}$ =x³ D、 $\frac{2 x y^{2}}{4 x^{2} y}$ = $\frac{1}{2}$

查看试题解析
4. 一个等腰三角形的两边长分别为4，8，则它的周长为（）

A、12 B、16 C、20 D、16或20

查看试题解析
5. 化简 $\frac{x^{2}}{x - 2} + \frac{4}{2 - x}$ 的结果是（）

A、x﹣2 B、 $\frac{1}{x - 2}$ C、 $\frac{x^{2} + 4}{x - 2}$ D、x+2

查看试题解析
6. 一件工作，甲独做a小时完成，乙独做b小时完成，则甲，乙两人合作完成需要（）小时．

A、 $\frac{1}{a} + \frac{1}{b}$ B、 $\frac{1}{a b}$ C、 $\frac{1}{a + b}$ D、 $\frac{a b}{a + b}$

查看试题解析
7. 如图（1），是一个长为2a宽为2b（a＞b）的矩形，用剪刀沿矩形的两条对角轴剪开，把它分成四个全等的小矩形，然后按图（2）拼成一个新的正方形，则中间空白部分的面积是（）

A、ab B、（a+b）² C、（a﹣b）² D、a²﹣b²

查看试题解析
8. 如图，△ABC中，AE是∠BAC的角平分线，AD是BC边上的高线，且∠B=50°，∠C=60°，则∠EAD的度数（）

A、35° B、5° C、15° D、25°

查看试题解析
9. 如图，在Rt△ABC中，∠ACB=90°，点D在AB边上，将△CBD沿CD折叠，使点B恰好落在AC边上的点E处，若∠A=26°，则∠CDE度数为（）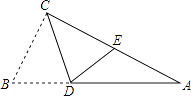

A、71° B、64° C、80° D、45°

查看试题解析
10. 如图，已知△ABC，求作一点P，使P到∠A的两边的距离相等，且PA=PB，下列确定P点的方法正确的是（）

A、P是∠A与∠B两角平分线的交点 B、P为∠A的角平分线与AB的垂直平分线的交点 C、P为AC，AB两边上的高的交点 D、P为AC，AB两边的垂直平分线的交点

查看试题解析
11. 如图，把一张矩形纸片ABCD沿对角线AC折叠，点B的对应点为B′，AB′与DC相交于点E，则下列结论一定正确的是（）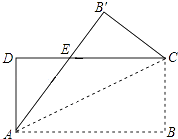

A、∠DAB′=∠CAB′ B、∠ACD=∠B′CD C、AD=AE D、AE=CE

查看试题解析
12. 如图，在Rt△ABC中，∠C=90°，∠CAB的平分线交BC于D，DE是AB的垂直平分线，垂足为E．若BC=3，则DE的长为（）

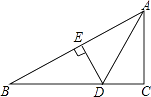A、1 B、2 C、3 D、4

查看试题解析
13. 如图，在△ABC中，BD，CD分别平分∠ABC，∠ACB，过点D作直线平行于BC，交AB，AC于点E，F，当∠A的位置及大小变化时，线段EF和BE+CF的大小关系为（）

A、EF＞BE+CF B、EF=BE+CF C、EF＜BE+CF D、不能确定

查看试题解析

二、填空题：

14. 在实数范围内因式分解：x³﹣2x²y+xy²= ．

查看试题解析
15. 计算：（ $\frac{1}{a} + \frac{1}{b}$ ）²÷（ $\frac{1}{a^{2}}$ ﹣ $\frac{1}{b^{2}}$ ）= ．

查看试题解析
16. 如图，在△ABC中，∠C=90°，∠B=30°，AB的垂直平分线ED交AB于点E，交BC于点D，若CD=3，则BD的长为．

查看试题解析
17.
如图，L是四边形ABCD的对称轴，如果AD∥BC，有下列结论：

(1)、①AB∥CD；②AB=CD；③AB⊥BC；④AO=OC
其中正确的结论是（把你认为正确的结论的序号都填上）．

查看试题解析
18. 如图，在等腰三角形纸片ABC中，AB=AC，∠A=40°，折叠该纸片，使点A落在点B处，折痕为DE，则∠CBE=°．

查看试题解析

三、解答题：

19. 计算下列各题

(1)、解方程： $\frac{1}{x - 2}$ ﹣3= $\frac{x - 1}{2 - x}$ ；

(2)、已知4x=3y，求代数式（x﹣2y）²﹣（x﹣y）（x+y）﹣2y²的值．

查看试题解析
20. 供电局的电力维修工要到30千米远的郊区进行电力抢修．技术工人骑摩托车先走，15分钟后，抢修车装载着所需材料出发，结果他们同时到达．已知抢修车的速度是摩托车的1.5倍，求这两种车的速度？

查看试题解析
21. 在等边三角形ABC中，点P在△ABC内，点Q在△ABC外，且∠ABP=∠ACQ，BP=CQ．

(1)、求证：△ABP≌△CAQ；

(2)、请判断△APQ是什么形状的三角形？试说明你的结论．

查看试题解析
22. 如图，在等边△ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F，

(1)、求∠F的度数；

(2)、若CD=3，求DF的长．

查看试题解析
23. 如图，在△ABC中，∠B=∠C=45°，点D在BC边上，点E在AC边上，且∠ADE=∠AED，连结DE．

(1)、当∠BAD=60°，求∠CDE的度数；

(2)、当点D在BC（点B、C除外）边上运动时，试写出∠BAD与∠CDE的数量关系，并说明理由．

查看试题解析
24. 如图，在△ABC中，AB=AC，DE是过点A的直线，BD⊥DE于D，CE⊥DE于点E；

(1)、若B、C在DE的同侧（如图所示）且AD=CE．求证：AB⊥AC；

(2)、若B、C在DE的两侧（如图所示），其他条件不变，AB与AC仍垂直吗？若是请给出证明；若不是，请说明理由．

查看试题解析