2016-2017学年内蒙古呼伦贝尔市满洲里市八年级上学期期末数学试卷
试卷更新日期:2017-03-13 类型:期末考试
一、选择题
-
1. 要使分式 有意义,x的取值范围满足( )A、x≠0 B、x=0 C、x>0 D、x<02. 下列大学的校徽图案是轴对称图形的是( )A、
 清华大学
B、
清华大学
B、 北京大学
C、
北京大学
C、 中国人民大学
D、
中国人民大学
D、 浙江大学
3. 下列计算正确的是( )A、(2x)2=2x2 B、x2•x3=x6 C、x5÷x3=x2 D、(x﹣2)3=x﹣54. 下列四个图形中,线段BE是△ABC的高的是( )A、
浙江大学
3. 下列计算正确的是( )A、(2x)2=2x2 B、x2•x3=x6 C、x5÷x3=x2 D、(x﹣2)3=x﹣54. 下列四个图形中,线段BE是△ABC的高的是( )A、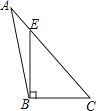 B、
B、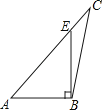 C、
C、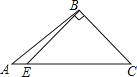 D、
D、 5. 下列等式从左到右的变形,属于因式分解的是( )A、a(x﹣y)=ax﹣ay B、x2+2x+1=x(x+2)+1 C、(x+1)(x+3)=x2+4x+3 D、x3﹣x=x(x+1)(x﹣1)6. 如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为( )
5. 下列等式从左到右的变形,属于因式分解的是( )A、a(x﹣y)=ax﹣ay B、x2+2x+1=x(x+2)+1 C、(x+1)(x+3)=x2+4x+3 D、x3﹣x=x(x+1)(x﹣1)6. 如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为( ) A、40° B、35° C、30° D、25°7. 已知点P(1,a)与Q(b,2)关于x轴成轴对称,则a﹣b的值为( )A、﹣1 B、1 C、﹣3 D、38. 分式 中的x,y都扩大2倍,则分式的值( )A、不变 B、扩大2倍 C、扩大4倍 D、缩小2倍9. 如图,△ABC中,AB=AC,∠C=72°,AB的垂直平分线DE交AC于D,交AB于E,则∠BDC的度数为( )
A、40° B、35° C、30° D、25°7. 已知点P(1,a)与Q(b,2)关于x轴成轴对称,则a﹣b的值为( )A、﹣1 B、1 C、﹣3 D、38. 分式 中的x,y都扩大2倍,则分式的值( )A、不变 B、扩大2倍 C、扩大4倍 D、缩小2倍9. 如图,△ABC中,AB=AC,∠C=72°,AB的垂直平分线DE交AC于D,交AB于E,则∠BDC的度数为( ) A、36° B、60° C、72° D、82°10. 如图所示,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS中( )
A、36° B、60° C、72° D、82°10. 如图所示,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS中( ) A、全部正确 B、仅①和③正确 C、仅①正确 D、仅①和②正确
A、全部正确 B、仅①和③正确 C、仅①正确 D、仅①和②正确二、填空题
-
11. 北京时间2011年3月11日,日本近海发生9.0级强烈地震.本次地震导致地球当天自转快了0.0000016秒.这里的0.0000016秒请你用科学记数法表示为秒.12. 三角形的两条边长是2和5,则第三条边a取值范围是 .13. 如图是某中学某班的班徽设计图案,其形状可以近似看做为正五边形,则每一个内角为度.
 14. 若多项式a2+6a+m是一个完全平方式,则m的值是 .15. 计算(π﹣3)0+( )﹣1= .16. 如图是一副三角尺拼成图案,则∠AEB=度.
14. 若多项式a2+6a+m是一个完全平方式,则m的值是 .15. 计算(π﹣3)0+( )﹣1= .16. 如图是一副三角尺拼成图案,则∠AEB=度. 17. 分解因式:3x2﹣6xy+3y2= .18. 如图,Rt△ABC中,∠B=90°,∠A=30°,AB=5,D是AC的中点,P是AB上一动点,则CP+PD的最小值为 .
17. 分解因式:3x2﹣6xy+3y2= .18. 如图,Rt△ABC中,∠B=90°,∠A=30°,AB=5,D是AC的中点,P是AB上一动点,则CP+PD的最小值为 .
三、解答题
-
19. 计算:(2a3•3a﹣2a)÷(﹣2a)20. 计算:21. 解方程: ﹣ =1.22. 先化简( ﹣ )÷ ,再选取一个你喜欢的x值求值.23. 已知:如图,A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF,
求证:△ABC≌△DEF.
 24. 已知:如图,在△ABC中,点A的坐标为(﹣4,3),点B的坐标为(﹣3,1),BC=2,BC∥x轴.
24. 已知:如图,在△ABC中,点A的坐标为(﹣4,3),点B的坐标为(﹣3,1),BC=2,BC∥x轴. (1)、画出△ABC关于y轴对称的图形△A1B1C1;并写出A1 , B1 , C1的坐标;(2)、求以点A、B、B1、A1为顶点的四边形的面积.
(1)、画出△ABC关于y轴对称的图形△A1B1C1;并写出A1 , B1 , C1的坐标;(2)、求以点A、B、B1、A1为顶点的四边形的面积.四、应用题
-
25. 为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
五、计算与证明