2016-2017学年河北省唐山市滦县九年级上学期期末数学试卷
试卷更新日期:2017-03-13 类型:期末考试
一、选择题
-
1. 方程x2+2x=3的根是( )A、x1=1,x2=﹣3 B、x1=﹣1,x2=3 C、x1=﹣1+ ,x2=﹣1﹣ D、x1=1+ ,x2=1﹣2. 如图,由下列条件不能判定△ABC与△ADE相似的是( )
 A、 = B、∠B=∠ADE C、 = D、∠C=∠AED3. 如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )
A、 = B、∠B=∠ADE C、 = D、∠C=∠AED3. 如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )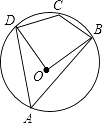 A、88° B、92° C、106° D、136°4. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
A、88° B、92° C、106° D、136°4. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:甲
乙
丙
丁
平均数(cm)
185
180
185
180
方差
3.6
3.6
7.4
8.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁5. 已知Rt△ABC中,∠C=90°,AC=3,BC=4,若以2为半径作⊙C,则斜边AB与⊙C的位置关系是( )A、相交 B、相切 C、相离 D、无法确定6. 反比例函数y= 的两个点为(x1 , y1)、(x2 , y2),且x1>x2>0,则下式关系成立的是( )A、y1>y2 B、y1<y2 C、y1=y2 D、不能确定7. 已知⊙O的半径为1,点A到圆心O的距离为a,若关于x的方程x2﹣2x+a=0不存在实数根,则点A与⊙O的位置关系是( )A、点A在⊙O外 B、点A在⊙O上 C、点A在⊙O内 D、无法确定8. 如图,已知⊙O的半径为5,弦AB=6,M是AB上任意一点,则线段OM的长可能是( ) A、2.5 B、3.5 C、4.5 D、5.59. 反比例函数y= 的图象如图所示,以下结论:
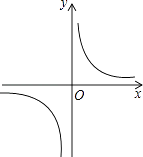
A、2.5 B、3.5 C、4.5 D、5.59. 反比例函数y= 的图象如图所示,以下结论:①常数m<﹣1;
②在每个象限内,y随x的增大而增大;
③若A(﹣1,h),B(2,k)在图象上,则h<k;
④若P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上.
其中正确的是( )
 A、①② B、②③ C、③④ D、①④10. 如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,CD⊥AB于D,设∠ACD=α,则cosα的值为( )
A、①② B、②③ C、③④ D、①④10. 如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,CD⊥AB于D,设∠ACD=α,则cosα的值为( )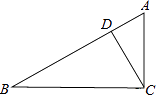 A、 B、 C、 D、11. 如图,函数y=ax2+bx+c(a≠0)的图象与x轴相交于A、B两点,頂点为点M.则下列说法不正确的是( )
A、 B、 C、 D、11. 如图,函数y=ax2+bx+c(a≠0)的图象与x轴相交于A、B两点,頂点为点M.则下列说法不正确的是( ) A、a<0 B、当x=﹣1时,函数y有最小值4 C、对称轴是直线=﹣1 D、点B的坐标为(﹣3,0)12. 如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长为( )
A、a<0 B、当x=﹣1时,函数y有最小值4 C、对称轴是直线=﹣1 D、点B的坐标为(﹣3,0)12. 如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长为( ) A、6cm B、7cm C、8cm D、9cm13. 如图,AB是⊙O的直径,弦CD⊥AB,∠C=30°,CD=2 .则S阴影=( )
A、6cm B、7cm C、8cm D、9cm13. 如图,AB是⊙O的直径,弦CD⊥AB,∠C=30°,CD=2 .则S阴影=( ) A、π B、2π C、 D、 π14. 如图,AD=DF=FB,DE∥FG∥BC,且把三角形ABC分成面积为S1 , S2 , S3三部分,则S1:S2:S3=( )
A、π B、2π C、 D、 π14. 如图,AD=DF=FB,DE∥FG∥BC,且把三角形ABC分成面积为S1 , S2 , S3三部分,则S1:S2:S3=( ) A、1:2:3 B、1:4:9 C、1:3:5 D、无法确定15. 如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,则GH长为( )
A、1:2:3 B、1:4:9 C、1:3:5 D、无法确定15. 如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,则GH长为( ) A、1 B、1.2 C、2 D、2.516. 如图,抛物线y1=a(x+2)2﹣3与y2= (x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
A、1 B、1.2 C、2 D、2.516. 如图,抛物线y1=a(x+2)2﹣3与y2= (x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2﹣y1=4;
④2AB=3AC;
其中正确结论是( )
 A、①② B、②③ C、③④ D、①④
A、①② B、②③ C、③④ D、①④二、填空题
-
17. 一台机器原价60万元,两年后这台机器的价格为48.6万元,如果每年的折旧率相同,则这台机器的折旧率为 .18. 如图,已知O是坐标原点,以O点为位似中心在y轴的左侧将△OBC放大两倍(即新图与原图的相似比为2),则B(3,﹣1)的对称点的坐标为 .
 19. 如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的直径是 cm.
19. 如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的直径是 cm. 20. 如图,把抛物线y= x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= x2交于点Q,则图中阴影部分的面积为 .
20. 如图,把抛物线y= x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= x2交于点Q,则图中阴影部分的面积为 .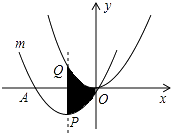
三、解答题
-
21. 如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y= 的图象的两个交点.
 (1)、求反比例函数和一次函数的解析式;(2)、求△AOB的面积;(3)、根据图象直接写出不等式kx+b< 时x的解集.22. 小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为45°,35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.(结果保留整数)
(1)、求反比例函数和一次函数的解析式;(2)、求△AOB的面积;(3)、根据图象直接写出不等式kx+b< 时x的解集.22. 小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为45°,35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.(结果保留整数)(参考数据:sin35°≈ ,cos35°≈ ,tan35°≈ )
 23. 某校260名学生参加植树活动,要求每人植4﹣7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成扇形图(如图(1))和条形图(如图(2)),经确认扇形图是正确的,而条形图尚有一处错误.
23. 某校260名学生参加植树活动,要求每人植4﹣7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成扇形图(如图(1))和条形图(如图(2)),经确认扇形图是正确的,而条形图尚有一处错误.回答下列问题:
 (1)、写出条形图中存在的错误,并说明理由;(2)、写出这20名学生每人植树量的众数、中位数;(3)、在求这20名学生每人植树量的平均数时,小宇是这样分析的:
(1)、写出条形图中存在的错误,并说明理由;(2)、写出这20名学生每人植树量的众数、中位数;(3)、在求这20名学生每人植树量的平均数时,小宇是这样分析的:第一步:求平均数的公式是 = ;
第二步:在该问题中,n=4,x1=4,x2=5,x3=6,x4=7;
第三步: = =5.5(份)
①小宇的分析是从哪一步开始出现错误的?
②请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵.
24. 某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.设每个房间每天的定价增加x元.求:
(1)、房间每天的入住量y(间)关于x(元)的函数关系式;(2)、该宾馆每天的房间收费p(元)关于x(元)的函数关系式;(3)、该宾馆客房部每天的利润w(元)关于x(元)的函数关系式;当每个房间的定价为每天多少元时,w有最大值?最大值是多少?25. 已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E. (1)、求证:DE是⊙O的切线;(2)、若DE=6cm,AE=3cm,求⊙O的半径.(3)、在(2)的条件下,直接写出tan∠CAB的值.26.
(1)、求证:DE是⊙O的切线;(2)、若DE=6cm,AE=3cm,求⊙O的半径.(3)、在(2)的条件下,直接写出tan∠CAB的值.26.如图,抛物线L:y=﹣ (x﹣t)(x﹣t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y= (k>0,x>0)于点P,且OA•MP=12.
 (1)、求k的值;(2)、当t=1时,求AB长,并求直线MP与L对称轴之间的距离;(3)、把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标.
(1)、求k的值;(2)、当t=1时,求AB长,并求直线MP与L对称轴之间的距离;(3)、把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标.