2016-2017学年河北省秦皇岛市抚宁学区九年级上学期期末数学试卷

试卷更新日期：2017-03-13 类型：期末考试

进入出卷网下载

一、选择题

1. 下列方程中是一元二次方程的是（）

A、xy+2=1 B、 $x^{2} + \frac{1}{2 x} - 9 = 0$ C、x²=0 D、ax²+bx+c=0

查看试题解析
2. 如图，在▱ABCD中，EF∥AB，DE：EA=2：3，EF=4，则CD的长为（）

A、 $\frac{16}{3}$ B、8 C、10 D、16

查看试题解析
3. 已知⊙O的半径为10cm，弦AB∥CD，AB=12cm，CD=16cm，则AB和CD的距离为（）

A、2cm B、14cm C、2cm或14cm D、10cm或20cm

查看试题解析
4. 粮仓顶部是圆锥形，这个圆锥的底面直径为4m，母线长为3m，为防雨需在仓顶部铺上油毡，这块油毡面积是（）

A、6m² B、6πm² C、12m² D、12πm²

查看试题解析
5. 若反比例函数y=（2m﹣1） $x^{m^{2} - 2}$ 的图象在第二，四象限，则m的值是（）

A、﹣1或1 B、小于 $\frac{1}{2}$ 的任意实数 C、﹣1 D、不能确定

查看试题解析
6. 在李咏主持的“幸运52”栏目中，曾有一种竞猜游戏，游戏规则是：在20个商标牌中，有5个商标牌的背面注明了一定的奖金，其余商标牌的背面是一张“哭脸”，若翻到“哭脸”就不获奖，参与这个游戏的观众有三次翻牌的机会，且翻过的牌不能再翻．有一位观众已翻牌两次，一次获奖，一次不获奖，那么这位观众第三次翻牌获奖的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{2}{9}$ C、 $\frac{1}{4}$ D、 $\frac{5}{18}$

查看试题解析
7. 抛物线y=3x²先向上平移2个单位，再向右平移3个单位，所得的抛物线为（）

A、y=3（x+3）²﹣2 B、y=3（x+3）²+2 C、y=3（x﹣3）²﹣2 D、y=3（x﹣3）²+2

查看试题解析
8. 如图，铁路道口的栏杆短臂长1m，长臂长16m．当短臂端点下降0.5m时，长臂端点升高（杆的宽度忽略不计）（）

A、4m B、6m C、8m D、12m

查看试题解析
9. 已知反比例函数y= $\frac{a b}{x}$ ，当x＞0时，y随x的增大而增大，则关于x的方程ax²﹣2x+b=0的根的情况是（）

A、有两个正根 B、有两个负根 C、有一个正根一个负根 D、没有实数根

查看试题解析
10. 如图是以△ABC的边AB为直径的半圆O，点C恰好在半圆上，过C作CD⊥AB交AB于D．已知cos∠ACD= $\frac{3}{5}$ ，BC=4，则AC的长为（）

A、1 B、 $\frac{20}{3}$ C、3 D、 $\frac{16}{3}$

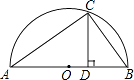查看试题解析
11. 如图，P为⊙O外一点，PA、PB分别切⊙O于A、B，CD切⊙O于点E，分别交PA、PB于点C、D，若PA=5，则△PCD的周长为（）

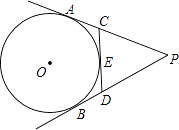A、5 B、7 C、8 D、10

查看试题解析
12. 如图，两个半径都是4cm的圆外切于点C，一只蚂蚁由点A开始依次A、B、C、D、E、F、C、G、A这8段路径上不断爬行，直到行走2006πcm后才停下来，则蚂蚁停的那一个点为（）

A、D点 B、E点 C、F点 D、G点

查看试题解析

二、填空题

13. 某农户2010年的年收入为4万元，由于“惠农政策”的落实，2012年年收入增加到5.8万元．设每年的年增长率x相同，则可列出方程为．

查看试题解析
14. 反比例函数y= $\frac{k}{x}$ （k＞0）在第一象限内的图象如图，点M是图象上一点MP垂直x轴于点P，如果△MOP的面积为1，那么k的值是．

查看试题解析
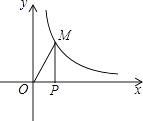15. 已知：如图，矩形ABCD的长和宽分别为2和1，以D为圆心，AD为半径作AE弧，再以AB的中点F为圆心，FB长为半径作BE弧，则阴影部分的面积为．

查看试题解析
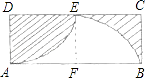16. 如图所示，⊙M与x轴相交于点A（2，0），B（8，0），与y轴相切于点C，则圆心M的坐标是．

查看试题解析
17. 如图，直线MN与⊙O相切于点M，ME=EF且EF∥MN，则cos∠E= ．

查看试题解析
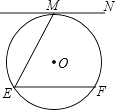18. 如图，△ABC是等腰直角三角形，BC是斜边，将△ABP绕点A逆时针旋转后，能与△ACP′重合，如果AP=3，那么PP′= ．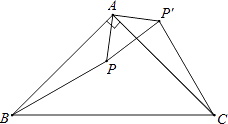

查看试题解析

三、解答题

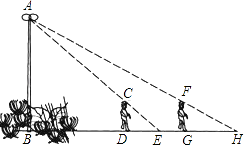
19. 已知a是锐角，且sin（a+15°）= $\frac{\sqrt{3}}{2}$ ，计算 $\sqrt{8}$ ﹣4cosα﹣（π﹣3.14）⁰+tanα+ ${(\frac{1}{3})}^{- 1}$ 的值．

查看试题解析
20. 已知反比例函数 $y = \frac{k}{x}$ 的图象经过点 $(4 ， \frac{1}{2})$ ，若一次函数y=x+1的图象平移后经过该反比例函数图象上的点B（2，m），求平移后的一次函数图象与x轴的交点坐标．

查看试题解析
21. 某商场将进价为30元的台灯以40元售出，平均每月能售出600个，调查表明：这种台灯的售价每上涨1元，其销售量就减少10个．

(1)、为了实现平均每月10000元的销售利润，商场决定采取调控价格的措施，扩大销售量，减少库存，这种台灯的售价应定为多少？这时应进台灯多少个？

(2)、如果商场要想每月的销售利润最多，这种台灯的售价又将定为多少？这时应进台灯多少个？

查看试题解析
22. 甲转盘的三个等分区域分别写有数字1、2、3，乙转盘的四个等分区域分别写有数字4、5、6、7．现分别转动两个转盘，通过画树形图或者列表法求指针所指数字之和为偶数的概率．

查看试题解析
23. 如图，花丛中有一路灯杆AB．在灯光下，小明在D点处的影长DE=3米，沿BD方向行走到达G点，DG=5米，这时小明的影长GH=5米．如果小明的身高为1.7米，求路灯杆AB的高度（精确到0.1米）．

查看试题解析
24. 如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连结DE．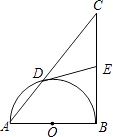

(1)、DE与半圆O相切吗？若相切，请给出证明；若不相切，请说明理由；

(2)、若AD、AB的长是方程x²﹣10x+24=0的两个根，求直角边BC的长．

查看试题解析
25.
如图，抛物线与x轴交于A（1，0）、B（﹣3，0）两点，与y轴交于点C（0，3），设抛物线的顶点为D．

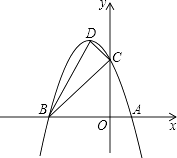(1)、求该抛物线的解析式与顶点D的坐标．

(2)、试判断△BCD的形状，并说明理由．

(3)、探究坐标轴上是否存在点P，使得以P，A，C为顶点的三角形与△BCD相似？若存在，请直接写出点P的坐标；若不存在，请说明理由．

查看试题解析