2016-2017学年河北省保定市定州市九年级上学期期末数学试卷
试卷更新日期：2017-03-13 类型：期末考试
一、选择题
-
1. 已知反比例函数y= 的图象经过点（3，2），那么下列四个点中，也在这个函数图象上的是（ ）A、（3，﹣2） B、（﹣2，﹣3） C、（1，﹣6） D、（﹣6，1）2. 抛物线y=（x+2）2+1的顶点坐标是（ ）A、（2，1） B、（2，﹣1） C、（﹣2，1） D、（﹣2，﹣1）3. 如果两个相似三角形对应边的比为2：3，那么这两个相似三角形面积的比是（ ）A、2：3 B、 ： C、4：9 D、8：274. 在一个不透明的口袋中，有大小、形状完全相同，颜色不同的球15个，从中摸出红球的概率为 ，则袋中红球的个数为（ ）A、10 B、15 C、5 D、35. 如图，一个宽为2 cm的刻度尺在圆上移动，当刻度尺的一边与圆相切时，另一边与圆两个交点处的读数恰好为“2”和“8”（单位：cm），那么该圆的半径为（ ）
A、 cm B、 cm C、3cm D、 cm6. 下列说法正确的是（ ）A、“任意画一个三角形，其内角和是360°”是随机事件 B、“明天的降水概率为80%”，意味着明天降雨的可能性较大 C、“某彩票中奖概率是1%”，表示买100张这种彩票一定会中奖 D、晓芳抛一枚硬币10次，有7次正面朝上，当她抛第11次时，正面向上的概率为7. 一元二次方程x2+ax+b=0的两个根分别为2和﹣3，那么（ ）A、a=2，b=﹣3 B、a=﹣3，b=2 C、a=1，b=﹣6 D、a=﹣1，b=68. 如图，在平行四边形ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF：FC等于（ ）
A、3：2 B、3：1 C、1：1 D、1：29.如图，在正方形ABCD中，E为DC边上的点，连接BE，将△BCE绕点C顺时针方向旋转90°得到△DCF，连接EF，若∠BEC=60°，则∠EFD的度数为（ ）
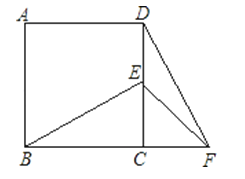A、10° B、15° C、20° D、25°10. 如图，各正方形的边长均为1，则四个阴影三角形中，一定相似的一对是（ ）
A、①② B、①③ C、②③ D、②④11. 如图，正比例函数y1=k1x的图象与反比例函数y2= 的图象相交于A，B两点，其中点A的横坐标为2，当y1＞y2时，x的取值范围是（ ）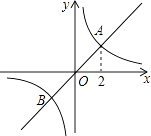
A、x＜﹣2或x＞2 B、x＜﹣2或0＜x＜2 C、﹣2＜x＜0或0＜x＜2 D、﹣2＜x＜0或x＞212. 如图所示，已知抛物线C1、C2关于x轴对称，抛物线C1 ， C3关于y轴对称，如果抛物线C2的解析式是y=﹣ （x﹣2）2+2，那么抛物线C3的解析式是（ ）
A、y=﹣ （x﹣2）2﹣2 B、y=﹣ （x+2）2+2 C、y= （x﹣2）2﹣2 D、y= （x+2）2﹣2二、填空题
-
13. 一元二次方程x2=3x的解是： ．14. 二次函数y=3x2﹣6x﹣3图象的对称轴是 ．15. 如图，点P、Q是反比例函数y= 图象上的两点，PA⊥y轴于点A，QN⊥x轴于点N，作PM⊥x轴于点M，QB⊥y轴于点B，连接PB、QM，△ABP的面积记为S1 ， △QMN的面积记为S2 ， 则S1S2 ． （填“＞”或“＜”或“=”）
16. 如图，在△ABC中，AB=5，D、E分别是边AC和AB上的点，且∠ADE=∠B，DE=2，那么AD•BC= ．
17. 已知，如图，AB是⊙O的直径，CA与⊙O相切于点A，连接CO交⊙O于点D，CO的延长线交⊙O于点E，连接BE、BD，∠ABD=35°，则∠C=度．
18. 如图，P是抛物线y=x2﹣4x+3上的一点，以点P为圆心、1个单位长度为半径作⊙P，当⊙P与直线y=0相切时，点P的坐标为 ．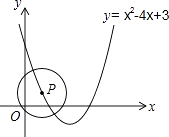
三、解答题
-
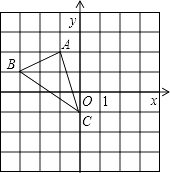
19. 解方程(1)、7x（5x+2）=6（5x+2）(2)、4x2﹣8x+1=0．20. 如图，若将△ABC绕点C逆时针旋转90°后得到△A′B′C′，
(1)、在图中画出△A′B′C′；(2)、求出点A经过的路径长．21. 已知关于x的方程 x2﹣（2k﹣1）x+k2=0(1)、若原方程有实数根，求k的取值范围？(2)、选取一个你喜欢的非零整数值作为k的值，使原方程有实数根，并解方程．22. 如图，已知反比例函数y= 与一次函数y=x+b的图象在第一象限相交于点A（1，﹣k+4）．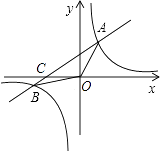
(1)、试确定这两个函数的表达式；(2)、求出这两个函数图象的另一个交点B的坐标，并求△AOB的面积．23. 某公司举行一个游戏，规则如下：有4张背面相同的卡片，分别对应1000元、600元、400元、200元的奖金，现将4张纸牌洗匀后背面朝上摆放到桌上，让员工抽取，每人有两次抽奖机会，两次抽取的奖金之和作为公司发的奖金．现有两种抽取的方案：①小芳抽取方案是：直接从四张牌中抽取两张．②小明抽取的方案是：先从四张牌中抽取一张后放回去，再从四张中再抽取一张．你认为是小明抽到的奖金不少于1000元的概率大还是小芳抽取到的奖金少于1000元的概率大？请用树形图或列表法进行分析说明．24. 已知：A是以BC为直径的圆上的一点，BE是⊙O的切线，CA的延长线与BE交于E点，F是BE的中点，延长AF，CB交于点P．
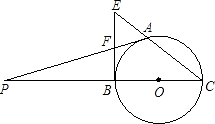(1)、求证：PA是⊙O的切线；(2)、若AF=3，BC=8，求AE的长．25. 某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施．调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台．(1)、假设每台冰箱降价x元，商场每天销售这种冰箱的利润是y元，请写出y与x之间的函数表达式；（不要求写自变量的取值范围）(2)、商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？(3)、每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？26. 如图，在△ABC中，BA=BC=20cm，AC=30cm，点P从A出发，沿AB以4cm/s的速度向点B运动；同时点Q从C点出发，沿CA以3cm/s的速度向A点运动．设运动时间为x（s）．
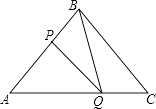(1)、当x为何值时，PQ∥BC；(2)、当△APQ与△CQB相似时，AP的长为；(3)、当S△BCQ：S△ABC=1：3，求S△APQ：S△ABQ的值．