备考2019年高考数学一轮专题:第13讲 导数与函数的单调性
试卷更新日期:2018-10-25 类型:一轮复习
一、单选题
-
1. 函数 的单调递减区间是( )A、 B、 与 C、 与 D、2. 若函数 在区间 内单调递增,则实数 的取值范围是( )
A、 B、 C、 D、3. 定义在R上的函数f(x)的导函数为f′(x),f(0)=0.若对任意x∈R,都有f(x)>f′(x)+1,则使得f(x)+ex<1成立的x的取值范围为( )A、(﹣∞,0) B、(﹣∞,1) C、(﹣1,+∞) D、(0,+∞)4. 函数 的单调递减区间为( )A、(-1,1) B、 C、(0,1) D、5. 已知函数 恰有两个零点,则实数 的取值范围是( )A、 B、 C、 D、6. 若幂函数f(x)的图象过点 ,则函数g(x)=exf(x)的单调递减区间为( )
A、(-∞,0) B、(-∞,-2) C、(-2,-1) D、(-2,0)7. 若函数 在区间 上单调递增,则k的取值范围是( )A、 B、 C、 D、8. 函数 的单调增区间是( )A、 B、 C、 . D、9. 函数 的单调减区间为( ) A、
的单调减区间为( ) A、 ,
,  B、
B、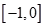 ,
, 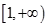 C、
C、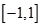 D、
D、 ,
, 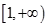 10. 已知f(x)=aln x+ x2(a>0),若对任意两个不等的正实数x1 , x2都有 恒成立,则实数a的取值范围是( )
10. 已知f(x)=aln x+ x2(a>0),若对任意两个不等的正实数x1 , x2都有 恒成立,则实数a的取值范围是( )
A、[1,+∞) B、(1,+∞) C、(0,1) D、(0,1]二、填空题
-
11. 已知函数f(x)=x2+3x-2ln x,则函数f(x)的单调递减区间为 .
12. 函数y=ax3﹣1在(﹣∞,+∞)上是减函数,则实数a的取值范围为 .13. 若函数f(x)=- x3+ x2+2ax在 上存在单调递增区间,则a的取值范围是 .
14. 已知函数f(x)= x2+2ax-lnx,若f(x)在区间 上是增函数,则实数a的取值范围为 .15. 已知函数 ,则函数的单调减区间为.16. 已知函数 ,若 ,则实数 的取值范围是 .三、解答题
-
17. 已知函数(1)、若a=3,求 的单调区间(2)、证明: 只有一个零点18. 已知函数 .(1)、求 的单调区间和极值;(2)、若直线 是函数 图象的一条切线,求 的值.19. 已知函数 .(1)、讨论 在 上的单调性;(2)、若 , ,求正数 的取值范围.