2016-2017学年安徽省滁州市天长市九年级上学期期末数学试卷
试卷更新日期:2017-03-13 类型:期末考试
一、选择题
-
1. 如果将抛物线y=x2+3向下平移1个单位,那么所得新抛物线的解析式是( )A、y=(x﹣1)2+3 B、y=(x+1)2+3 C、y=x2+2 D、y=x2+42. 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的 后得到线段CD,则端点C的坐标为( )
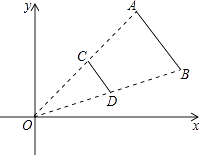 A、(3,3) B、(4,3) C、(3,1) D、(4,1)3. 如图,某水库堤坝横断面迎水坡AB的斜面坡度是1: ,堤坝高BC=50m,则迎水坡面AB的长度是( )
A、(3,3) B、(4,3) C、(3,1) D、(4,1)3. 如图,某水库堤坝横断面迎水坡AB的斜面坡度是1: ,堤坝高BC=50m,则迎水坡面AB的长度是( )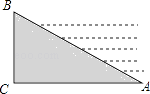 A、100m B、120m C、50 m D、100 m4. 如图所示,△ABC中,∠BAC=32°,将△ABC绕点A按顺时针方向旋转55°,对应得到△AB′C′,则∠B′AC的度数为( )
A、100m B、120m C、50 m D、100 m4. 如图所示,△ABC中,∠BAC=32°,将△ABC绕点A按顺时针方向旋转55°,对应得到△AB′C′,则∠B′AC的度数为( )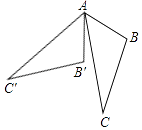 A、22° B、23° C、24° D、25°5. 将一副三角板按如图①的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,得到如图②,测得CG=6 ,则AC长是( )
A、22° B、23° C、24° D、25°5. 将一副三角板按如图①的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,得到如图②,测得CG=6 ,则AC长是( ) A、6+2 B、9 C、10 D、6+66. 如图,在△ABC中,D、E分别是AB、AC的中点,下列说法中不正确的是( )
A、6+2 B、9 C、10 D、6+66. 如图,在△ABC中,D、E分别是AB、AC的中点,下列说法中不正确的是( )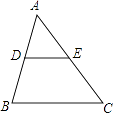 A、DE= BC B、 C、△ADE∽△ABC D、S△ADE:S△ABC=1:27. 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:
A、DE= BC B、 C、△ADE∽△ABC D、S△ADE:S△ABC=1:27. 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0
其中正确的个数为( )
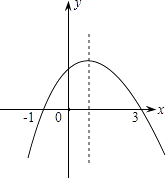 A、1 B、2 C、3 D、48. 如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
A、1 B、2 C、3 D、48. 如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( ) A、 B、 C、 D、9. 如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
A、 B、 C、 D、9. 如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )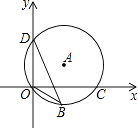 A、 B、 C、 D、10. 如图,在矩形ABCD中,AB=2,点E在边AD上,∠ABE=45°,BE=DE,连接BD,点P在线段DE上,过点P作PQ∥BD交BE于点Q,连接QD.设PD=x,△PQD的面积为y,则能表示y与x函数关系的图象大致是( )
A、 B、 C、 D、10. 如图,在矩形ABCD中,AB=2,点E在边AD上,∠ABE=45°,BE=DE,连接BD,点P在线段DE上,过点P作PQ∥BD交BE于点Q,连接QD.设PD=x,△PQD的面积为y,则能表示y与x函数关系的图象大致是( )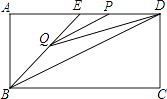 A、
A、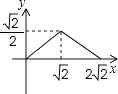 B、
B、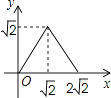 C、
C、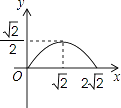 D、
D、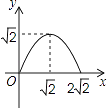
二、填空题
-
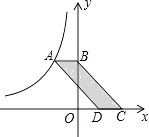
11. 如图,点A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C、D在x轴上,且BC∥AD,四边形ABCD的面积为3,则这个反比例函数的解析式为
 12. 如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降1米时,水面的宽度为米.
12. 如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降1米时,水面的宽度为米.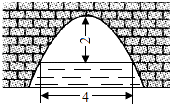 13. 如图,四边形ABCD内接于⊙O,∠DAB=130°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为度(写出一个即可).
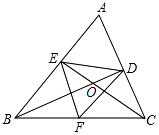
13. 如图,四边形ABCD内接于⊙O,∠DAB=130°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为度(写出一个即可).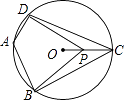 14. 如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点O,F为BC的中点,连接EF,DF,DE,则下列结论:①EF=DF;②AD•AC=AE•AB;③△DOE∽△COB;④若∠ABC=45°时,BE= FC.
14. 如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点O,F为BC的中点,连接EF,DF,DE,则下列结论:①EF=DF;②AD•AC=AE•AB;③△DOE∽△COB;④若∠ABC=45°时,BE= FC.其中正确的是(把所有正确结论的序号都选上)
三、解答题
-
15. 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y= 的图象交于A(2,3),B(﹣3,n)两点.
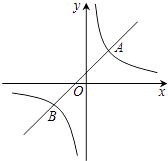 (1)、求一次函数和反比例函数的解析式;(2)、若P是y轴上一点,且满足△PAB的面积是5,直接写出点P的坐标.16. 如图,在边长为1个单位长度的小正方形组成的网格中.
(1)、求一次函数和反比例函数的解析式;(2)、若P是y轴上一点,且满足△PAB的面积是5,直接写出点P的坐标.16. 如图,在边长为1个单位长度的小正方形组成的网格中.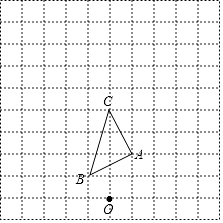 (1)、以图中的点O为位似中心,在网格中画出△ABC的位似图形△A1B1C1 , 使△A1B1C1与△ABC的位似比为2:1;(2)、若△A1B1C1的面积为S,则△ABC的面积是
(1)、以图中的点O为位似中心,在网格中画出△ABC的位似图形△A1B1C1 , 使△A1B1C1与△ABC的位似比为2:1;(2)、若△A1B1C1的面积为S,则△ABC的面积是四、解答题
-
17. 如图,在四边形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD交于点H.
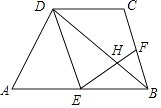 (1)、求证:△EDH∽△FBH;(2)、若BD=6,求DH的长.18. 如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.
(1)、求证:△EDH∽△FBH;(2)、若BD=6,求DH的长.18. 如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.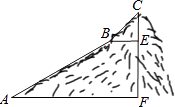 (1)、求AB段山坡的高度EF;(2)、求山峰的高度CF.( 1.414,CF结果精确到米)
(1)、求AB段山坡的高度EF;(2)、求山峰的高度CF.( 1.414,CF结果精确到米)五、解答题
-
19. 某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.(1)、求y与x的函数关系式,并写出自变量x的取值范围;(2)、顾客一次性购买多少件时,该网店从中获利最多?20. 如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.
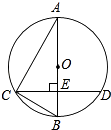 (1)、求证:∠ACO=∠BCD;(2)、若EB=8cm,CD=24cm,求⊙O的直径.
(1)、求证:∠ACO=∠BCD;(2)、若EB=8cm,CD=24cm,求⊙O的直径.六、解答题
-
21. 在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E,F分别是AC,BC边上一点.
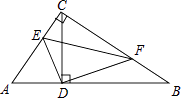 (1)、求证: ;(2)、若CE= AC,BF= BC,求∠EDF的度数.
(1)、求证: ;(2)、若CE= AC,BF= BC,求∠EDF的度数.七、解答题
-
22. 如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
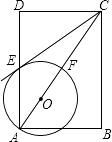 (1)、判断直线CE与⊙O的位置关系,并证明你的结论;(2)、若tan∠ACB= ,BC=2,求⊙O的半径.
(1)、判断直线CE与⊙O的位置关系,并证明你的结论;(2)、若tan∠ACB= ,BC=2,求⊙O的半径.八、解答题
-
23. 如图,在平面直角坐标系中,已知点A(10,0),B(4,8),C(0,8),连接AB,BC,点P在x轴上,从原点O出发,以每秒1个单位长度的速度向点A运动,同时点M从点A出发,以每秒2个单位长度的速度沿折线A﹣B﹣C向点C运动,其中一点到达终点时,另一点也随之停止运动,设P,M两点运动的时间为t秒.
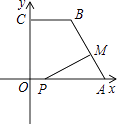 (1)、求AB长;(2)、设△PAM的面积为S,当0≤t≤5时,求S与t的函数关系式,并指出S取最大值时,点P的位置;(3)、t为何值时,△APM为直角三角形?
(1)、求AB长;(2)、设△PAM的面积为S,当0≤t≤5时,求S与t的函数关系式,并指出S取最大值时,点P的位置;(3)、t为何值时,△APM为直角三角形?
-
-