2016-2017学年安徽省亳州市九年级上学期期末数学试卷

试卷更新日期：2017-03-13 类型：期末考试

进入出卷网下载

一、选择题

1. 抛物线y=﹣（x﹣2）²+3的顶点坐标是（）

A、（﹣2，3） B、（2，3） C、（﹣2，﹣3） D、（2，﹣3）

查看试题解析
2. 下列各组中的四条线段成比例的是（）

A、1cm、2cm、20cm、30cm B、1cm、2cm、3cm、4cm C、5cm、10cm、10cm、20cm D、4cm、2cm、1cm、3cm

查看试题解析
3. 将抛物线y=﹣x²向左平移2个单位后，得到的抛物线的解析式是（）

A、y=﹣（x+2）² B、y=﹣x²+2 C、y=﹣（x﹣2）² D、y=﹣x²﹣2

查看试题解析
4. 在Rt△ABC中，若各边长都扩大3倍，则锐角A的正弦值（）

A、不变 B、扩大3倍 C、缩小到原来的 $\frac{1}{3}$ D、不能确定

查看试题解析
5. 将二次函数y= $\frac{1}{4}$ x²+x﹣1化为y=a（x+h）²+k的形式是（）

A、y= $\frac{1}{4} {(x + 2)}^{2} + 2$ B、y= $\frac{1}{4}$ （x﹣2）²﹣2 C、y= $\frac{1}{4}$ （x+2）²﹣2 D、y= $\frac{1}{4}$ （x﹣2）²+2

查看试题解析
6. 如图，在▱ABCD中若BE：EC=4：5，则BF：FD=（）

A、4：5 B、4：10 C、4：9 D、5：9

查看试题解析
7. 如图，点M是△ABC内一点，过点M分别作直线平行于△ABC的各边，所形成的三个小三角形△₁ ， △₂ ， △₃（图中阴影部分）的面积分别是4，9和16，则△ABC的面积是（）

A、49 B、64 C、100 D、81

查看试题解析
8. 已知P₁（x₁ ， y₁），P₂（x₂ ， y₂），P₃（x₃ ， y₃）是反比例函数y= $\frac{2}{x}$ 的图象上的三点，且x₁＜x₂＜0＜x₃ ，则y₁、y₂、y₃的大小关系是（）

A、y₃＜y₂＜y₁ B、y₂＜y₁＜y₃ C、y₁＜y₂＜y₃ D、y₂＜y₃＜y₁

查看试题解析
9. 如图，AB是斜靠在墙上的长梯，梯脚B距墙角1.4m，楼上点D距离墙1.2m，BD长0.5m，则梯子的长为（）

A、3.2m B、4m C、3.5m D、4.2m

查看试题解析
10. 二次函数y=ax²+bx+c（a≠0）的图象的对称轴是直线x=1，其图象的一部分如图所示则①abc＜0；②a﹣b+c＜0；③3a+c＜0；④当﹣1＜x＜3时，y＞0．其中判断正确的有（）个．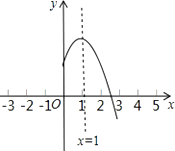

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 如图，P是∠α的边OA上一点，且点P的坐标为（3，4），则sinα= ．

查看试题解析
12. 试写出图象位于第二、四象限的一个反比例函数的解析式．

查看试题解析
13. 设点C是长度为8cm的线段AB的黄金分割点（AC＞BC），则AC的长为 cm．

查看试题解析
14. 如图，在△ABC中，AB=AC=10，点D是BC边上的一动点（不与B、C重合），∠ADE=∠B=∠α，DE交AB于点E，且tan∠α= $\frac{3}{4}$ ，有以下的结论：①△DBE∽△ACD；②△ADE∽△ACD；③△BDE为直角三角形时，BD为8或 $\frac{7}{2}$ ；④0＜BE≤5，其中正确的结论是（填入正确结论的序号）

查看试题解析
15. 已知a、b、c为△ABC的三边长，且a+b+c=36， $\frac{a}{3}$ = $\frac{b}{4}$ = $\frac{c}{5}$ ，求△ABC三边的长．

查看试题解析
16. 计算：|﹣2|+2sin30°﹣（﹣ $\sqrt{3}$ ）²+（tan45°）^﹣¹ ．

查看试题解析
17. 如图所示，在△ABC与△ADE中，AB•ED=AE•BC，要使△ABC与△ADE相似，还需要添加一个条件，这个条件是（只加一个即可）并证明．

查看试题解析
18. 如图，在边长为1个单位长度的小正方形组成的网格中，建立如图所示的平面直角坐标系，请按要求完成下面的问题：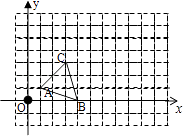

(1)、以图中的点O为位似中心，将△ABC作位似变换且同向放大到原来的两倍，得到△A₁B₁C₁；

(2)、若△ABC内一点P的坐标为（a，b），则位似变化后对应的点P′的坐标是．

查看试题解析
19. 如图，一次函数y₁=ax+b的图象与反比例函数y₂= $\frac{k}{x}$ 的图象交于M，N两点．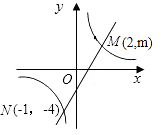

(1)、利用图中条件，求反比例函数和一次函数的解析式；

(2)、观察图象，比较y₁与y₂的大小．

查看试题解析
20. 如图，一艘海轮位于灯塔P的南偏东60°方向，距离灯塔40海里的A处，它计划沿正北方向航行，去往位于灯塔P的北偏东45°方向上的B处．问B处距离灯塔P有多远？（结果精确到0.1海里）
（参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732， $\sqrt{6}$ ≈2.449）

查看试题解析
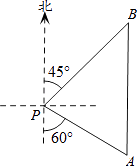21. 鄂州市化工材料经销公司购进一种化工原料若干千克，价格为每千克30元．物价部门规定其销售单价不高于每千克60元，不低于每千克30元．经市场调查发现：日销售量y（千克）是销售单价x（元）的一次函数，且当x=60时，y=80；x=50时，y=100．在销售过程中，每天还要支付其他费用450元．

(1)、求出y与x的函数关系式，并写出自变量x的取值范围．

(2)、求该公司销售该原料日获利w（元）与销售单价x（元）之间的函数关系式．

(3)、当销售单价为多少元时，该公司日获利最大？最大获利是多少元？

查看试题解析
22. 在直角坐标系中，已知点A（﹣2，0），B（0，4），C（0，3），过点C作直线交x轴于点D，使得以D，O，C为顶点的三角形与△AOB相似，求点D的坐标．

查看试题解析
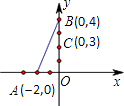23.
如图，抛物线y=ax²+bx+c（a＞0）的顶点为M，直线y=m与x轴平行，且与抛物线交于点A，B，若△AMB为等腰直角三角形，我们把抛物线上A，B两点之间的部分与线段AB围成的图形称为该抛物线对应的准碟形，线段AB称为碟宽，顶点M称为碟顶，点M到线段AB的剧烈为碟高．

(1)、抛物线y=x²对应的碟宽为；抛物线y= $\frac{1}{2}$ x²对应的碟宽为；抛物线y=ax²（a＞0）对应的碟宽为；抛物线y=a（x﹣3）²+2（a＞0）对应的碟宽为；

(2)、利用图（1）中的结论：抛物线y=ax²﹣4ax﹣ $\frac{5}{3}$ （a＞0）对应的碟宽为6，求抛物线的解析式．

(3)、将抛物线y_n=a_nx²+b_nx+c_n（a_n＞0）的对应准蝶形记为F_n（n=1，2，3，…），定义F₁ ， F₂ ， …..F_n为相似准蝶形，相应的碟宽之比即为相似比．若F_n与F_n_﹣₁的相似比为 $\frac{1}{2}$ ，且F_n的碟顶是F_n_﹣₁的碟宽的中点，现在将（2）中求得的抛物线记为y₁ ，其对应的准蝶形记为F₁ ．
①求抛物线y₂的表达式；
②若F₁的碟高为h₁ ， F₂的碟高为h₂ ， …F_n的碟高为h_n ．则h_n= ， F_n的碟宽右端点横坐标为．

查看试题解析