2017高考数学备考复习易错题九：空间向量与立体几何

试卷更新日期：2017-03-13 类型：三轮冲刺

进入出卷网下载

一、单选题

1.
如图，四棱锥P－ABCD中，底面ABCD是矩形，PD⊥平面ABCD，且PD＝AD＝1，AB＝2，点E是AB上一点，当二面角P－EC－D的平面角为 $\frac{π}{4}$ 时，AE＝(　　)

A、1 B、 $\frac{1}{2}$ C、2－ $\sqrt{2}$ D、2－ $\sqrt{3}$

查看试题解析
2. △ABC一边BC在平面 $α$ 内，顶点A在平面 $α$ 外，已知 $∠ A B C = \frac{π}{3}$ ，三角形所在平面与 $α$ 所成的二面角为 $\frac{π}{6}$ ，则直线AB与 $α$ 所成角的正弦值为( )

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{3}}{4}$

查看试题解析
3.
如图所示，正方体ABCD-A'B'C'D'的棱长为1，O是平面A'B'C'D'的中心，则O到平面ABC'D'的距离是（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{4}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
4. 如图，正方体ABCD-A₁B₁C₁D₁的棱长为1，线段B₁D₁上有两个动点E，F，且EF= $\frac{\sqrt{2}}{2}$ ，则下列结论中错误的个数是( )

(1) AC⊥BE.
(2) 若P为AA₁上的一点，则P到平面BEF的距离为 $\frac{\sqrt{2}}{2}$ .
(3) 三棱锥A-BEF的体积为定值.
(4) 在空间与DD₁ ， AC，B₁C₁都相交的直线有无数条.
(5) 过CC₁的中点与直线AC₁所成角为40并且与平面BEF所成角为50的直线有2条.

A、0 B、1 C、2 D、3

查看试题解析
5. 已知 $\vec{A B} = (1 ， 5 ， - 2)$ ， $\vec{B C} = (3 ， 1 ， z)$ ，若 $\vec{A B} ⊥ \vec{B C}$ ， $\vec{B P} = (x - 1 ， y ， - 3)$ 且BP $⊥$ 平面ABC，则实数x，y，z分别为( )

A、 $\frac{33}{7} ， - \frac{15}{7} ， 4$ B、 $\frac{40}{7} ， - \frac{15}{7} ， 4$ C、 $\frac{40}{7} ， - 2 ， 4$ D、 $4 ， \frac{40}{7} ， - 15$

查看试题解析
6. 若平面α、β的法向量分别为 $\vec{n_{1}}$ =（2，﹣3，5）， $\vec{n_{2}}$ =（﹣3，1，﹣4），则（　　）

A、α∥β B、α⊥β C、α、β相交但不垂直 D、以上均不正确

查看试题解析
7. 已知正四棱柱ABCD﹣A₁B₁C₁D₁中，AA₁=2AB，则CD与平面BDC₁所成角的正弦值等于（　　）

A、 $\frac{2}{3}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{2}}{3}$ D、 $\frac{1}{3}$

查看试题解析
8. 以正方体ABCD﹣A₁B₁C₁D₁的顶点D为坐标原点O，如图建立空间直角坐标系，则与 $\vec{D B_{1}}$ 共线的向量的坐标可以是（）

A、（2，﹣2，2） B、（﹣2，﹣2，2） C、（﹣2，2，2） D、（﹣2，﹣2，﹣2）

查看试题解析
9. 如图长方体ABCD﹣A′B′C′D′中，AB=6，AD=D′D=5，二面角D′﹣AB﹣D的大小是（）

A、30° B、45° C、60° D、90°

查看试题解析
10. 在平行六面体ABCD﹣A₁B₁C₁D₁中，化简 $\vec{A B}$ + $\vec{A D}$ + $\vec{A A_{1}}$ =（　　）

A、 $\vec{A C_{1}}$ B、 $\vec{C A_{1}}$ C、 $\vec{B C_{1}}$ D、 $\vec{C B_{1}}$

查看试题解析

二、填空题

11. 已知向量 $\vec{O A} ⊥ \vec{A B} ，$ $|\vec{O A}| = 3$ ，则 $\vec{O A} \cdot \vec{O B} =$ ．

查看试题解析
12. 设点C（2a+1，a+1，2）在点设P（2，0，0），A（1，﹣3，2），B（8，﹣1，4）确定的平面上，则a的值为．

查看试题解析
13. 三棱锥P﹣ABC中，PA⊥平面ABC，PA=AB，则直线PB与平面ABC所成的角等于．

查看试题解析

三、综合题

14.
如图，已知正三棱锥P﹣ABC的侧面是直角三角形，PA=6，顶点P在平面ABC内的正投影为点D，D在平面PAB内的正投影为点E，连接PE并延长交AB于点G．

(1)、证明：G是AB的中点；

(2)、在图中作出点E在平面PAC内的正投影F（说明作法及理由），并求四面体PDEF的体积．

查看试题解析
15.
如图，在三棱台ABC﹣DEF中，平面BCFE⊥平面ABC，∠ACB=90°，BE=EF=FC=1，BC=2，AC=3．

(1)、求证：BF⊥平面ACFD；

(2)、求直线BD与平面ACFD所成角的余弦值．

查看试题解析
16.
如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点．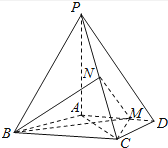

(1)、证明：MN∥平面PAB；

(2)、求直线AN与平面PMN所成角的正弦值．

查看试题解析
17. 如图，四棱锥P﹣ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB与△PAD都是等边三角形．

(1)、证明：PB⊥CD；

(2)、求二面角A﹣PD﹣C的大小．

查看试题解析
18. 如图，四棱柱ABCD﹣A₁B₁C₁D₁的底面ABCD是正方形，O为底面中心，A₁O⊥平面ABCD， $A B = A A_{1} = \sqrt{2}$ ．

(1)、证明：A₁C⊥平面BB₁D₁D；

(2)、求平面OCB₁与平面BB₁D₁D的夹角θ的大小．

查看试题解析
19. 如图，四边形ABCD为正方形．PD⊥平面ABCD，∠DPC=30°，AF⊥PC于点F，FE∥CD，交PD于点E．

(1)、证明：CF⊥平面ADF；

(2)、求二面角D﹣AF﹣E的余弦值．

查看试题解析
20. 如图，△ABC和△BCD所在平面互相垂直，且AB=BC=BD=2．∠ABC=∠DBC=120°，E、F分别为AC、DC的中点．

(1)、求证：EF⊥BC；

(2)、求二面角E﹣BF﹣C的正弦值．

查看试题解析
21.
如图，长方体ABCD﹣A₁B₁C₁D₁中，AA₁=AB=1，AD=2，E为BC的中点，点M，N分别为棱DD₁ ， A₁D₁的中点．

(1)、求证：平面CMN∥平面A₁DE；

(2)、求证：平面A₁DE⊥平面A₁AE．

查看试题解析

2017高考数学备考复习 易错题九：空间向量与立体几何

一、单选题

二、填空题

三、综合题

2017高考数学备考复习易错题九：空间向量与立体几何