2016-2017学年吉林省延边州安图县九年级上学期期末数学试卷
试卷更新日期:2017-03-13 类型:期末考试
一、选择题:
-
1. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一元二次方程2x2+8x=0的解是( )A、x1=x2=4 B、x1=x2=0 C、x1=0,x2=4 D、x1=0,x2=﹣43. 将抛物线y=x2向左平移5个单位后得到的抛物线对应的函数解析式是( )A、y=﹣x2+5 B、y=x2﹣5 C、y=(x﹣5)2 D、y=(x+5)24. 如图,⊙O的半径OB=1,弦AC=1,点D在⊙O上,则∠D的度数是( )
2. 一元二次方程2x2+8x=0的解是( )A、x1=x2=4 B、x1=x2=0 C、x1=0,x2=4 D、x1=0,x2=﹣43. 将抛物线y=x2向左平移5个单位后得到的抛物线对应的函数解析式是( )A、y=﹣x2+5 B、y=x2﹣5 C、y=(x﹣5)2 D、y=(x+5)24. 如图,⊙O的半径OB=1,弦AC=1,点D在⊙O上,则∠D的度数是( ) A、60° B、45° C、75° D、30°5. 已知反比例函数y= ,当1<x<3时,y的最小整数值是( )A、3 B、4 C、5 D、66. 在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )A、
A、60° B、45° C、75° D、30°5. 已知反比例函数y= ,当1<x<3时,y的最小整数值是( )A、3 B、4 C、5 D、66. 在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )A、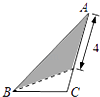 B、
B、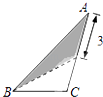 C、
C、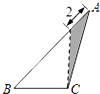 D、
D、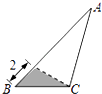
二、填空题:
-
7. 数学老师将全班分成6个小组开展小组合作学习,采用随机抽签确定一个小组进行展示活动,则第3个小组被抽到的概率是 .8. 若 = ,则 = .9. 一元二次方程(x﹣5)(2x﹣1)=3的根的判别式的值是 .10. 在平面直角坐标系中,抛物线y=(x+2)2﹣3与y轴的交点坐标是 .11. 如图,△ABC∽△DEF,AB=3,DE=2,若△DEF的周长为8,则△ABC的周长为 .
 12. 如图,在△ABC中,DE∥BC,若 = ,DE=9,则BC的长为 .
12. 如图,在△ABC中,DE∥BC,若 = ,DE=9,则BC的长为 . 13. 如图,AB是⊙O的直径,点C,D,E,F在⊙O上,且点C,D和点E,F分别是半圆的三等分点,点P,Q在AB上,连接PC、PD、QE、QF,若⊙O的半径为2,则图中阴影部分图形的面积和为(结果保留π).
13. 如图,AB是⊙O的直径,点C,D,E,F在⊙O上,且点C,D和点E,F分别是半圆的三等分点,点P,Q在AB上,连接PC、PD、QE、QF,若⊙O的半径为2,则图中阴影部分图形的面积和为(结果保留π).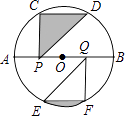 14. 如图,在平面直角坐标系中,△OAB的顶点A,B的坐标分别为(4,0)、(4,n),若经过点O、A的抛物线y=﹣x2+bx+c的顶点C落在边OB上,则图中阴影部分图形的面积和为 .
14. 如图,在平面直角坐标系中,△OAB的顶点A,B的坐标分别为(4,0)、(4,n),若经过点O、A的抛物线y=﹣x2+bx+c的顶点C落在边OB上,则图中阴影部分图形的面积和为 .
三、解答题:
-
15. 解方程:x2+4x﹣1=0.16. 如图,有三张背面完全相同的纸牌A,B,C,其中正面分别画有三种不同的几何图形,小华将这3张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张,请你用画树状图或列表的方法,求摸出的两张纸牌面上所画几何图形既是轴对称图形又是中心对称图形的概率.
 17. 如图,在△ABC中,D是AC边上一点,且AD=2DC,E是AB边上一点,ED与BC的延长线相交于点F,且BC=CF,G是EF的中点,连接CG,若CG=2,求AB的长.
17. 如图,在△ABC中,D是AC边上一点,且AD=2DC,E是AB边上一点,ED与BC的延长线相交于点F,且BC=CF,G是EF的中点,连接CG,若CG=2,求AB的长.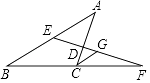 18. 已知反比例函数y= (k常数,k≠1).(1)、若点A(2,1)在这个函数的图象上,求k的值;(2)、若在这个函数图象的每一个分支上,y随x的增大而增大,求k的取值范围;(3)、若k=9,试判断点B(﹣ ,﹣16)是否在这个函数的图象上,并说明理由.
18. 已知反比例函数y= (k常数,k≠1).(1)、若点A(2,1)在这个函数的图象上,求k的值;(2)、若在这个函数图象的每一个分支上,y随x的增大而增大,求k的取值范围;(3)、若k=9,试判断点B(﹣ ,﹣16)是否在这个函数的图象上,并说明理由.四、解答题:
-
19. 如图,在平面直角坐标系中,△OAB的顶点坐标分别为(0,0),A(2,1),B(1,﹣2).
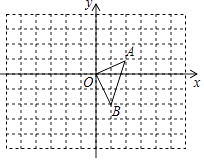 (1)、以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1 , 使它与△OAB的位似比为2:1,并分别写出点A,B的对应点A1、B1的坐标;(2)、画出将△OAB向左平移2个单位,再向上平移1个单位后得△O2A2B2 , 并写出点A,B的对应点A2、B2的坐标;(3)、判断△OA1B1和△O2A2B2是位似图形吗?若是,请在图中标出位似中心 M,并写出点M的坐标.20. 为进一步发展基础教育,自2014年以来,某县加大了教育经费的投入,2014年该县投入教育经费6000万元,并规划投入教育经费逐年增加,2016年在2014年的基础上增加投入教育经费2640万元,设该县这两年投入教育经费的年平均增长率相同,求这两年该县投入教育经费的年平均增长率.21. 如图,在平面直角坐标系中,点O为坐标原点,平移抛物线y=x2﹣2x+3,使平移后的抛物线经过点A(﹣2,0),且与y轴交于点B,同时满足以A,O,B为顶点的三角形是等腰直角三角形,求平移后的抛物线的解析式.
(1)、以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1 , 使它与△OAB的位似比为2:1,并分别写出点A,B的对应点A1、B1的坐标;(2)、画出将△OAB向左平移2个单位,再向上平移1个单位后得△O2A2B2 , 并写出点A,B的对应点A2、B2的坐标;(3)、判断△OA1B1和△O2A2B2是位似图形吗?若是,请在图中标出位似中心 M,并写出点M的坐标.20. 为进一步发展基础教育,自2014年以来,某县加大了教育经费的投入,2014年该县投入教育经费6000万元,并规划投入教育经费逐年增加,2016年在2014年的基础上增加投入教育经费2640万元,设该县这两年投入教育经费的年平均增长率相同,求这两年该县投入教育经费的年平均增长率.21. 如图,在平面直角坐标系中,点O为坐标原点,平移抛物线y=x2﹣2x+3,使平移后的抛物线经过点A(﹣2,0),且与y轴交于点B,同时满足以A,O,B为顶点的三角形是等腰直角三角形,求平移后的抛物线的解析式.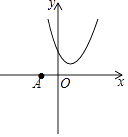 22. 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,过点D作DE⊥AB于点E.
22. 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,过点D作DE⊥AB于点E. (1)、求证:DE是⊙O的切线;(2)、若AC=10,BC=16,求DE的长.
(1)、求证:DE是⊙O的切线;(2)、若AC=10,BC=16,求DE的长.五、解答题:
-
23. 如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,﹣1),反比例函数y= (x>0)的图象经过线段MN的中点A.
 (1)、求直线l和反比例函数的解析式;(2)、在函数y= (x>0)的图象上取不同于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P,若△ONP的面积是△OBC的面积的3倍,求点P的坐标.24. 在矩形ABCD中,AD=3,CD=4,点E在边CD上,且DE=1.
(1)、求直线l和反比例函数的解析式;(2)、在函数y= (x>0)的图象上取不同于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P,若△ONP的面积是△OBC的面积的3倍,求点P的坐标.24. 在矩形ABCD中,AD=3,CD=4,点E在边CD上,且DE=1. (1)、感知:如图①,连接AE,过点E作EF⊥AE,交BC于点F,连接AF,易证:△ADE≌△ECF(不需要证明);(2)、探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE∽△ECF;(3)、应用:如图③,若EF交AB边于点F,其他条件不变,且△PEF的面积是3,则AP的长为 .
(1)、感知:如图①,连接AE,过点E作EF⊥AE,交BC于点F,连接AF,易证:△ADE≌△ECF(不需要证明);(2)、探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE∽△ECF;(3)、应用:如图③,若EF交AB边于点F,其他条件不变,且△PEF的面积是3,则AP的长为 .六、解答题:
-
25. 如图,已知A,B两点的坐标分别为(40,0)和(0,30),动点P从点A开始在线段AO上以每秒2个长度单位的速度向原点O运动、动直线EF从x轴开始以每1个单位的速度向上平行移动(即EF∥x轴),并且分别与y轴、线段AB交于点E,F,连接EP,FP,设动点P与动直线EF同时出发,运动时间为t秒.
 (1)、求t=15时,△PEF的面积;(2)、直线EF、点P在运动过程中,是否存在这样的t,使得△PEF的面积等于160(平方单位)?若存在,请求出此时t的值;若不存在,请说明理由.(3)、当t为何值时,△EOP与△BOA相似.26. 如图①,抛物线y=ax2+bx+c与x轴正半轴交于A、B两点,与y轴交于点C,直线y=﹣x+2经过A、C两点,且AB=2.
(1)、求t=15时,△PEF的面积;(2)、直线EF、点P在运动过程中,是否存在这样的t,使得△PEF的面积等于160(平方单位)?若存在,请求出此时t的值;若不存在,请说明理由.(3)、当t为何值时,△EOP与△BOA相似.26. 如图①,抛物线y=ax2+bx+c与x轴正半轴交于A、B两点,与y轴交于点C,直线y=﹣x+2经过A、C两点,且AB=2.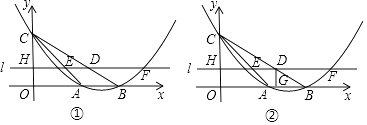 (1)、求抛物线的解析式;(2)、若直线l平行于x轴,直线l从点C出发以每秒1个单位长度的速度沿y轴负半轴方向向点O运动,到点O停止,且分别交线段AC、线段BC、抛物线、y轴于点E、D、F(点F在对称轴的右侧)、H,当点D是线段EF的三等分点时,求t的值;(3)、如图②,在直线l运动的过程中,过点D作x轴的垂线交x轴于点G,四边形OHDG与△AOC重叠部分的面积为S,求S与t的函数关系式.
(1)、求抛物线的解析式;(2)、若直线l平行于x轴,直线l从点C出发以每秒1个单位长度的速度沿y轴负半轴方向向点O运动,到点O停止,且分别交线段AC、线段BC、抛物线、y轴于点E、D、F(点F在对称轴的右侧)、H,当点D是线段EF的三等分点时,求t的值;(3)、如图②,在直线l运动的过程中,过点D作x轴的垂线交x轴于点G,四边形OHDG与△AOC重叠部分的面积为S,求S与t的函数关系式.