2016-2017学年河南省漯河市召陵区九年级上学期期末数学试卷

试卷更新日期：2017-03-13 类型：期末考试

进入出卷网下载

一、选择题

1. 一元二次方程2x（3x﹣2）=（x﹣1）（3x﹣2）的解是（）

A、x=﹣1 B、x= $\frac{2}{3}$ C、x₁= $\frac{2}{3}$ ，x₂=0 D、x₁= $\frac{2}{3}$ ，x₂=﹣1

查看试题解析
2. y= $\sqrt{k - 1}$ x+1是关于x的一次函数，则一元二次方程kx²+2x+1=0的根的情况为（）

A、没有实数根 B、有一个实数根 C、有两个不相等的实数根 D、有两个相等的实数根

查看试题解析
3. 如图，正六边形ABCDEF内接于⊙O，⊙O的半径为4，则这个正六边形的边心距OM和 $\hat{B C}$ 的长分别为（）

A、2， $\frac{4 π}{3}$ B、 $\sqrt{3}$ ，π C、2 $\sqrt{3}$ ， $\frac{8 π}{3}$ D、2 $\sqrt{3}$ ， $\frac{4 π}{3}$

查看试题解析
4. 已知反比例函数y=﹣ $\frac{2}{x}$ ，下列结论不正确的是（　　）

A、图象必经过点（﹣1，2） B、y随x的增大而增大 C、图象在第二、四象限内 D、若x＞1，则y＞﹣2

查看试题解析
5. 如图，△ABC中，AB=6，BC=4，将△ABC绕点A逆时针旋转得到△AEF，使得AF∥BC，延长BC交AE于点D，则线段CD的长为（）

A、4 B、5 C、6 D、7

查看试题解析
6. 如图，在平面直角坐标系中，过格点A，B，C作一圆弧，点B与下列格点的连线中，能够与该圆弧相切的是（）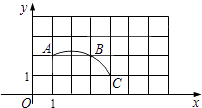

A、点（0，3） B、点（2，3） C、点（5，1） D、点（6，1）

查看试题解析
7.
矩形OABC在平面直角坐标系中的位置如图所示，点B的坐标为（3，4），D是OA的中点，点E在AB上，当△CDE的周长最小时，点E的坐标为（）

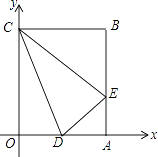A、（3，1） B、（3， $\frac{4}{3}$ ） C、（3， $\frac{5}{3}$ ） D、（3，2）

查看试题解析
8. 在平面直角坐标系中，函数y=x²﹣2x（x≥0）的图象为C₁ ， C₁关于原点对称的图象为C₂ ，则直线y=a（a为常数）与C₁、C₂的交点共有（）

A、1个 B、1个或2个 C、1个或2个或3个 D、1个或2个或3个或4个

查看试题解析

二、填空题

9. a、b、c是实数，点A（a+1、b）、B（a+2，c）在二次函数y=x²﹣2ax+3的图象上，则b、c的大小关系是bc（用“＞”或“＜”号填空）

查看试题解析
10. 从数﹣2，﹣ $\frac{1}{2}$ ，0，4中任取一个数记为m，再从余下的三个数中，任取一个数记为n，若k=mn，则正比例函数y=kx的图象经过第三、第一象限的概率是．

查看试题解析
11. 正比例函数y₁=mx（m＞0）的图象与反比例函数y₂= $\frac{k}{x}$ （k≠0）的图象交于点A（n，4）和点B，AM⊥y轴，垂足为M．若△AMB的面积为8，则满足y₁＞y₂的实数x的取值范围是．

查看试题解析
12. 如图，△ABC中，AC=6，AB=4，点D与点A在直线BC的同侧，且∠ACD=∠ABC，CD=2，点E是线段BC延长线上的动点，当△DCE和△ABC相似时，线段CE的长为．

查看试题解析
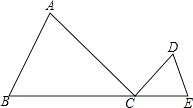13. 如图，AC是半圆O的一条弦，以弦AC为折线将弧AC折叠后过圆心O，⊙O的半径为2，则圆中阴影部分的面积为．

查看试题解析
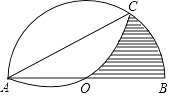14. 如图，P是⊙O外一点，PA和PB分别切⊙O于A、B两点，已知⊙O的半径为6cm，∠PAB=60°，若用图中阴影部分以扇形围成一个圆锥的侧面，则这个圆锥的高为．

查看试题解析
15. 矩形纸片ABCD，AB=9，BC=6，在矩形边上有一点P，且DP=3．将矩形纸片折叠，使点B与点P重合，折痕所在直线交矩形两边于点E，F，则EF长为．

查看试题解析

三、解答题

16. 父亲节快到了，明明准备为爸爸煮四个大汤圆作早点：一个芝麻馅，一个水果馅，两个花生馅，四个汤圆除内部馅料不同外，其它一切均相同．

(1)、求爸爸吃前两个汤圆刚好都是花生馅的概率；

(2)、若给爸爸再增加一个花生馅的汤圆，则爸爸吃前两个汤圆都是花生馅的可能性是否会增大？请说明理由．

查看试题解析
17. 在如图的网格图中，每个小正方形的边长均为1个单位，在Rt△ABC中，∠C=90°，AC=3，BC=4．

(1)、试在图中做出△ABC以A为旋转中心，沿顺时针方向旋转90°后的图形△AB₁C₁；

(2)、若点B的坐标为（﹣3，5），试在图中画出平面直角坐标系，并标出A、C两点的坐标；

(3)、根据（2）的坐标系，以B为位似中心，做△BA₂C₂ ，使△BA₂C₂与△ABC位似，且△BA₂C₂与△ABC位似比为2：1，并直接写出A₂的坐标．

查看试题解析
18. 如图，已知AC、EC分别为四边形ABCD和EFCG的对角线，点E在△ABC内，∠CAE+∠CBE=90°，当四边形ABCD和EFCG均为正方形时，连接BF．

(1)、求证：△CAE∽△CBF；

(2)、若BE=1，AE=2，求CE的长．

查看试题解析
19. 如图1，反比例函数y= $\frac{k}{x}$ （x＞0）的图象经过点A（2 $\sqrt{3}$ ，1），射线AB与反比例函数图象交于另一点B（1，a），射线AC与y轴交于点C，∠BAC=75°，AD⊥y轴，垂足为D．

(1)、求k的值；

(2)、求tan∠DAC的值及直线AC的解析式；

(3)、如图2，
M是线段AC上方反比例函数图象上一动点，过M作直线l⊥x轴，与AC相交于点N，连接CM，求△CMN面积的最大值．

查看试题解析
20. 如图，在Rt△ABC中，∠ABC=90°，AB=CB，以AB为直径的⊙O交AC于点D，点E是AB边上一点（点E不与点A、B重合），DE的延长线交⊙O于点G，DF⊥DG，且交BC于点F．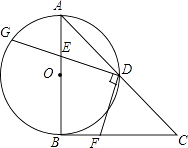

(1)、求证：AE=BF；

(2)、连接GB，EF，求证：GB∥EF；

(3)、若AE=1，EB=2，求DG的长．

查看试题解析
21. 旅游公司在景区内配置了50辆观光车供游客租赁使用，假定每辆观光车一天内最多能出租一次，且每辆车的日租金x（元）是5的倍数，发现每天的营运规律如下：当x不超过100元时，观光车能全部租出；当x超过100元时，每辆车的日租金每增加5元，租出去的观光车就会减少1辆，已知所有观光车每天的管理费是1100元．

(1)、优惠活动期间，为使观光车全部租出且每天的净收入为正，则每辆车的日租金至少应为多少元？（注：净收入=租车收入﹣管理费）

(2)、设每日净收入为w元，请写出w与x之间的函数关系式；

(3)、若某日的净收入为4420元，且使游客得到实惠，则当天的观光车的日租金是多少元？

查看试题解析
22.
问题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，试判断BE、EF、FD之间的数量关系．

(1)、【发现证明】
小聪把△ABE绕点A逆时针旋转90°至△ADG，从而发现EF=BE+FD，请你利用图1证明上述结论．

(2)、【类比引申】
如图2，四边形ABCD中∠BAD≠90°，AB=AD，∠B+∠D=180°，点E、F分别在边BC、CD上，则当∠EAF与∠BAD满足什么关系时，仍有EF=BE+FD

(3)、【探究应用】如图3，在某公园的同一水平面上，四条通道围成的ABCD，已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分别有景点E、F，且AE⊥AD，DF=40（ $\sqrt{3} - 1)$ ，米，现要在E、F之间修一条笔直道路，求这条道路EF的长（结果取整数，参考数据： $\sqrt{2}$ =1.41， $\sqrt{3}$ =1.73）．

查看试题解析
23.
如图，抛物线y=ax²+bx+c的图象经过点A（﹣2，0），点B（4，0），点D（2，4），与y轴交于点C，作直线BC，连接AC，CD．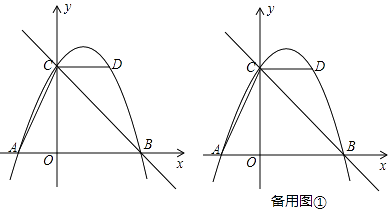

(1)、求抛物线的函数表达式；

(2)、E是抛物线上的点，求满足∠ECD=∠ACO的点E的坐标；

(3)、点M在y轴上且位于点C上方，点N在直线BC上，点P为第一象限内抛物线上一点，若以点C，M，N，P为顶点的四边形是菱形，求菱形的边长．

查看试题解析