2017高考数学备考复习易错题五：平面向量

试卷更新日期：2017-03-13 类型：三轮冲刺

进入出卷网下载

一、单选题

1. 对于向量a，b，e及实数x，y，x₁ ， x₂ ， $λ$ ，给出下列四个条件：
① $a + b = 3 e$ 且 $a - b = 5 e$ ； ② $x_{1} a + x_{2} b = 0$
③ $a = λ b (b \neq 0)$ 且 $λ$ 唯一； ④ $x a + y b = 0 (x + y = 0)$
其中能使a与b共线的是 ( )

A、①② B、②④ C、①③ D、③④

查看试题解析
2. 已知 $A$ 、 $B$ 、 $C$ 三点不共线，点 $O$ 为平面 $A B C$ 外的一点，则下列条件中，能得出 $M \in$ 平面 $A B C$ 的条件是（）

A、 $\vec{O M} = \frac{1}{2} \vec{O A} + \frac{1}{2} \vec{O B} + \frac{1}{2} \vec{O C}$ B、 $\vec{O M} = \frac{1}{3} \vec{O A} - \frac{1}{3} \vec{O B} + \vec{O C}$ C、 $\vec{O M} = \vec{O A} + \vec{O B} + \vec{O C}$ D、 $\vec{O M} = 2 \vec{O A} - \vec{O B} - \vec{O C}$

查看试题解析
3. 已知点 $A$ ， $B$ ， $C$ 在圆 $x^{2} + y^{2} = 1$ 上运动，且 $A B ⊥ B C$ ，若点 $P$ 的坐标为 $(2, 0)$ ，则 $|\vec{P A} + \vec{P B} + \vec{P C}|$ 的最大值为（）

A、6 B、7 C、8 D、9

查看试题解析
4.
若，则等于（）.

A、- $\frac{1}{2}$ $\vec{a}$ + $\frac{3}{2}$ $\vec{b}$ B、 $\frac{1}{2}$ $\vec{a}$ - $\frac{3}{2}$ $\vec{b}$ C、 $\frac{3}{2}$ $\vec{a}$ - $\frac{1}{2}$ $\vec{b}$ D、- $\frac{3}{2}$ $\vec{a}$ + $\frac{1}{2}$ $\vec{b}$

查看试题解析
5.
已知向量 $\vec{a}$ =(1-sin $θ$ ， 1）， $\vec{b}$ =（ $\frac{1}{2}$ ， 1+sin $θ$ ），且 $\vec{a}$ 平行于 $\vec{b}$ ，则锐角θ等于（）

A、30° B、45° C、60° D、75°

查看试题解析
6.
如图所示，等腰梯形ABCD中，对角线AC与BD交于点P，点E，F分别在两腰AD，BC上，EF过点P，且EF∥AB，则下列等式成立的是( )

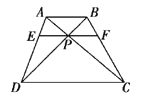A、 $\vec{A D}$ = $\vec{B C}$ B、 $\vec{A C}$ = $\vec{B D}$ C、 $\vec{P E}$ = $\vec{P F}$ D、 $\vec{E P}$ = $\vec{P F}$

查看试题解析
7. 已知M（x₀ ， y₀）是双曲线C： $\frac{x^{2}}{2}$ -y²=1上的一点，F₁ ， F₂是C上的两个焦点，若 $\vec{M F_{1}} \cdot \vec{M F_{2}} < 0$ ，则y₀的取值范围是( )

A、(- $\frac{\sqrt{3}}{3}$ ， $\frac{\sqrt{3}}{3}$ ) B、(- $\frac{\sqrt{3}}{6}$ ， $\frac{\sqrt{3}}{6}$ ) C、(- $\frac{2 \sqrt{2}}{3}$ ， $\frac{2 \sqrt{2}}{3}$ ) D、(- $\frac{2 \sqrt{3}}{3}$ ， $\frac{2 \sqrt{3}}{3}$ )

查看试题解析
8. 设 $\vec{e_{1}}$ 与 $\vec{e_{2}}$ 是不共线的非零向量，且k $\vec{e_{1}}$ + $\vec{e_{2}}$ 与 $\vec{e_{1}}$ +k $\vec{e_{2}}$ 共线，则k的值是（　　）

A、1 B、-1 C、±1 D、任意不为零的实数

查看试题解析
9. △ABC中，点D、E、F分别为AB、BC、CA的中点，则 $\vec{A F}$ - $\vec{D B}$ =（　　）

A、 $\vec{F D}$ B、 $\vec{F C}$ C、 $\vec{F E}$ D、 $\vec{B E}$

查看试题解析
10. 已知向量 $\vec{B A}$ =（ $\frac{1}{2}$ ， $\frac{\sqrt{3}}{2}$ ）， $\vec{B C}$ =（ $\frac{\sqrt{3}}{2}$ ， $\frac{1}{2}$ ），则∠ABC=（　　）

A、30° B、45° C、60° D、120°

查看试题解析
11. 已知向量 $\vec{a} = (1 ， m) ， \vec{b} = (3 ， - 2)$ ，且 $(\vec{a} + \vec{b}) ⊥ \vec{b}$ ，则m=（）

A、－8 B、－6 C、6 D、8

查看试题解析
12. 平面上的向量 $\vec{M A}$ 与 $\vec{M B}$ 满足| $\vec{M A}$ |²+| $\vec{M B}$ |=4，且 $\vec{M A}$ $\cdot$ $\vec{M B}$ =0，若点C满足 $\vec{M C}$ = $\frac{1}{3}$ $\vec{M A}$ + $\frac{2}{3}$ $\vec{M B}$ ，则| $\vec{M C}$ |的最小值为（　　）

A、1 B、 $\frac{\sqrt{7}}{4}$ C、 $\frac{3}{4}$ D、 $\frac{\sqrt{5}}{4}$

查看试题解析
13. 设向量 $\vec{a}$ ， $\vec{b}$ 满足| $\vec{a}$ + $\vec{b}$ |= $\sqrt{10}$ ，| $\vec{a}$ ﹣ $\vec{b}$ |= $\sqrt{6}$ ，则 $\vec{a}$ • $\vec{b}$ =（）

A、1 B、2 C、3 D、5

查看试题解析
14. 下列命题正确的是（）

A、向量 $\vec{a}$ 与 $\vec{b}$ 不共线，则 $\vec{a}$ 与 $\vec{b}$ 都是非零向量 B、任意两个相等的非零向量的始点与终点是一平行四边形的四个顶点 C、 $\vec{a}$ 与 $\vec{b}$ 共线， $\vec{b}$ 与 $\vec{c}$ 共线，则 $\vec{a}$ 与 $\vec{c}$ 也共线 D、有相同起点的两个非零向量不平行

查看试题解析
15. 已知两个单位向量 $\vec{e_{1}} ， \vec{e_{2}}$ 的夹角为45°，且满足 $\vec{e_{1}}$ ⊥（λ $\vec{e_{2}}$ ﹣ $\vec{e_{1}}$ ），则实数λ的值为（）

A、1 B、 $\sqrt{2}$ C、 $\frac{2 \sqrt{3}}{3}$ D、2

查看试题解析

二、填空题

16. 已知向量 $\vec{O A} ⊥ \vec{A B} ，$ $|\vec{O A}| = 3$ ，则 $\vec{O A} \cdot \vec{O B} =$ ．

查看试题解析
17. 过点 $p (1 ， \sqrt{3})$ 作圆 $x^{2} + y^{2} = 1$ 的两条切线，切点分别为 $A ， B$ ，则 $A B$ · $P B$ = .

查看试题解析
18. 已知向量 $\vec{a}$ ， $\vec{b}$ ，| $\vec{a}$ |=1，| $\vec{b}$ |=2，若对任意单位向量 $\vec{e}$ ，均有| $\vec{a}$ • $\vec{e}$ |+| $\vec{b}$ • $\vec{e}$ |≤ $\sqrt{6}$ ，则 $\vec{a}$ • $\vec{b}$ 的最大值是．

查看试题解析
19.
如图，在△ABC中，D是BC的中点，E ， F是AD上的两个三等分点， $\vec{B C} \cdot \vec{C A}$ =4， $\vec{B F} \cdot \vec{C F}$ =﹣1，则 $\vec{B E} \cdot \vec{C E}$ 的值是.

查看试题解析

三、综合题

20. 设向量 $\vec{a}$ =（cosθ，sinθ）， $\vec{b}$ =（﹣ $\frac{1}{2}$ ， $\frac{\sqrt{3}}{2}$ ）；

(1)、若 $\vec{a}$ ∥ $\vec{b}$ ，且θ∈（0，π），求θ；

(2)、若|3 $\vec{a}$ + $\vec{b}$ |=| $\vec{a}$ ﹣3 $\vec{b}$ |，求| $\vec{a}$ + $\vec{b}$ |的值．

查看试题解析

2017高考数学备考复习 易错题五：平面向量

一、单选题

二、填空题

三、综合题

2017高考数学备考复习易错题五：平面向量