人教版七年级数学上册期中检测卷A

试卷更新日期：2018-10-24 类型：期中考试

进入出卷网下载

一、选择题

1. 有一个程序，当输入任意一个有理数时，显示屏上的结果总是1与输入的有理数的差的倒数，若第一次输入3，并将显示的结果第二次输入，则此时显示的结果是（）

A、3 B、 $- \frac{1}{2}$ C、 $\frac{2}{3}$ D、﹣3

查看试题解析
2. 我市今年参加中考人数约为42000人，将42000用科学记数法表示为（）

A、4.2×10⁴ B、0.42×10⁵ C、4.2×10³ D、42×10³

查看试题解析
3. 合并同类项m﹣3m+5m﹣7m+…+2013m的结果为（）

A、0 B、1007m C、m D、以上答案都不对

查看试题解析
4. 在数﹣（﹣3），0，﹣（+3），﹣|﹣3|，（﹣3）²中非负数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
5. 在式子 $\frac{a b}{3}$ ，﹣4x， $- \frac{7}{5}$ abc，π， $\frac{m - n}{2}$ ，0.81， $\frac{1}{y}$ ，0中，单项式共有（）

A、5个 B、6个 C、7个 D、8个

查看试题解析
6. 若ma=mb，那么下列等式不一定成立的是（）

A、ma+2=mb+2 B、a=b C、﹣ma=﹣mb D、ma﹣6=mb﹣6

查看试题解析
7. 方程2（1﹣x）= $\frac{1}{2}$ x的解是（）

A、x= $\frac{4}{3}$ B、x= $\frac{4}{5}$ C、x= $\frac{2}{3}$ D、x= $\frac{5}{4}$

查看试题解析
8. 下列计算正确的是（）

A、5a+2b=7ab B、5a³﹣3a²=2a C、4a²b﹣3ba²=a²b D、﹣ $\frac{1}{2}$ y²﹣ $\frac{1}{4}$ y²=﹣ $\frac{3}{4}$ y⁴

查看试题解析
9. 若有理数a、b在数轴上的位置如图所示，则下列各式中成立的是（）

A、a＜﹣b B、b﹣a＞0 C、|a|＜|b| D、a+b＞0

查看试题解析
10. 如图所示的运算程序中，如果开始输入的x值为﹣48，我们发现第1次输出的结果为﹣24，第2次输出的结果为﹣12，…，第2016次输出的结果为（）

A、﹣6 B、﹣3 C、﹣24 D、﹣12

查看试题解析

二、填空题

11. 已知：（a+2b）y²﹣y^a^﹣1=3是关于y的一元一次方程，则a+b的值为．

查看试题解析
12. 已知关于x的方程2ax=（a+1）x+3的解是正整数，则正整数a= ．

查看试题解析
13. 一般情况下 $\frac{m}{2} + \frac{n}{3} = \frac{m + n}{2 + 3}$ 不成立，但有些数可以使得它成立，例如：m=n=0时，我们称使得 $\frac{m}{2} + \frac{n}{3} = \frac{m + n}{2 + 3}$ 成立的一对数m，n为“相伴数对”，记为（m，n）．

(1)、若（m，1）是“相伴数对”，则m=；

(2)、（m，n）是“相伴数对”，则代数式 $\frac{15}{4}$ m﹣[n+ $\frac{1}{2}$ （6﹣12n﹣15m）]的值为．

查看试题解析
14. 电影《哈利•波特》中，小哈利波特穿越墙进入“ $9 \frac{3}{4}$ 站台”的镜头（如示意图的Q站台），构思奇妙，能给观众留下深刻的印象．若A、B站台分别位于﹣ $\frac{2}{3}$ ， $\frac{8}{3}$ 处，AP=2PB，则P站台用类似电影的方法可称为“站台”．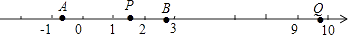

查看试题解析
15. 已知一个两位数A的十位数字是m，个位数字是n，一个三位数B的百位数字是n，十位数字和个位数字都是m，则B﹣A= ．

查看试题解析
16. 世界著名的莱布尼兹三角形如图所示，其排在第8行从左边数第3个位置上的数是．

查看试题解析

三、解答题

17. 对于有理数a、b，定义一种新运算“⊙”，规定：a⊙b=|a+b|+|a﹣b|．

(1)、计算2⊙（﹣4）的值；

(2)、若a，b在数轴上的位置如图所示，化简a⊙b．

查看试题解析
18. 计算：[（﹣ $\frac{9}{14}$ +1 $\frac{2}{7}$ ﹣ $\frac{5}{21}$ ]÷（﹣ $\frac{1}{42}$ ） $+ \frac{3}{2}$ ×|﹣1¹⁰﹣（﹣3）²|

查看试题解析
19. 若关于x的方程3（x+4）=2a+5的解大于关于x的方程 $\frac{(4 a + 1) x}{4} = \frac{a (3 x - 4)}{3}$ 的解，试确定a的取值范围．

查看试题解析

四、解答题（一）

20. 先化简，再求值：已知a²﹣1=0，求（5a²+2a﹣1）﹣2（a+a²）的值．

查看试题解析
21. 回答问题：

(1)、求整式（a²+4ab﹣5）的2倍与整式（a²﹣6ab+9）的差．

(2)、若（a﹣6）²+|b+ $\frac{2}{3}$ |=0，求（1）中所求整式的值．

查看试题解析
22. 如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动．它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走均为正，向下向左走均为负．如果从A到B记为：A→B（+1，+4），从B到A记为：B→A（﹣1，﹣4），其中第一个数表示左右方向，第二个数表示上下方向．

(1)、图中A→C（，），B→C（，），C→（+1，﹣2）；

(2)、若这只甲虫从A处去甲虫P处的行走路线依次为（+2，+2），（+2，﹣1），（﹣2，+3），（﹣1，﹣2），请在图中标出P的位置；

(3)、若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程．

(4)、若图中另有两个格点M、N，且M→A（3﹣a，b﹣4），M→N（5﹣a，b﹣2），则N→A应记为什么？

查看试题解析

五、解答题（二）

23. 某班准备买一些乒乓球和乒乓球拍，现了解情况如下：甲、乙两家商店出售同样品牌的乒乓球和乒乓球拍，乒乓球拍每副68元，乒乓球每盒12元．经商谈后，甲商店每买一副乒乓球拍赠一盒乒乓球，乙商店全部按定价的9折优惠．这个班级需要球拍5副，乒乓球x盒（x≥5）．

(1)、分别求甲、乙两家商店购买这些商品所需的费用（用含x的代数式表示）．

(2)、当x=40时，购买所需商品去哪家商店合算？请通过计算说明理由．

查看试题解析
24. 观察下列各式：
1×5+4=3²…………①
3×7+4=5²…………②
5×9+4=7²…………③
……
探索以上式子的规律：

(1)、试写出第6个等式；

(2)、试写出第n个等式（用含n的式子表示），并用你所学的知识说明第n个等式成立．

查看试题解析
25. 数轴上A 点对应的数为﹣5，B 点在A 点右边，电子蚂蚁甲、乙在B分别以2个单位/秒、1个单位/秒的速度向左运动，电子蚂蚁丙在A 以3个单位/秒的速度向右运动．

(1)、若电子蚂蚁丙经过5秒运动到C 点，求C点表示的数；

(2)、若它们同时出发，若丙在遇到甲后1秒遇到乙，求B 点表示的数；

(3)、在（2）的条件下，设它们同时出发的时间为t 秒，是否存在t 的值，使丙到乙的距离是丙到甲的距离的2倍？若存在，求出t值；若不存在，说明理由．

查看试题解析