人教版七年级数学上册 第四章几何图形初步 单元检测卷
试卷更新日期:2018-10-24 类型:单元试卷
一、选择题
-
1. 把弯曲的河道改直,能够缩短船舶航行的路程,这样做的道理是( )A、垂线段最短 B、两点确定一条直线 C、两点之间,直线最短 D、两点之间,线段最短2. 围成下列这些立体图形的各个面中,都是平的面为( )A、
 B、
B、 C、
C、 D、
D、 3. 下列四个图中,能用∠1、∠AOB、∠O三种方法表示同一个角的是( )A、
3. 下列四个图中,能用∠1、∠AOB、∠O三种方法表示同一个角的是( )A、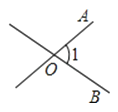 B、
B、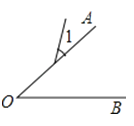 C、
C、 D、
D、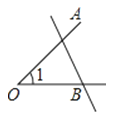 4. 下列关系式正确的是( )A、35.5°=35°5′ B、35.5°=35°50′ C、35.5°<35°5′ D、35.5°>35°5′5. 如图,点C是线段AB的中点,点D是线段CB的中点,下列说法错误的是( )
4. 下列关系式正确的是( )A、35.5°=35°5′ B、35.5°=35°50′ C、35.5°<35°5′ D、35.5°>35°5′5. 如图,点C是线段AB的中点,点D是线段CB的中点,下列说法错误的是( ) A、CD=AC-BD B、CD= AB-BD C、BC-BD, D、CD= AB6.
A、CD=AC-BD B、CD= AB-BD C、BC-BD, D、CD= AB6.分别从一个几何体的正面、左面、上面观察得到的平面图形如图所示,则这个几何体是( )
 A、圆柱 B、圆锥 C、球 D、棱柱7. 用一副三角板不能画出( )A、75°角 B、135°角 C、160°角 D、105°角8. 下列叙述正确的是( )A、180°是补角 B、120°和60°互为补角 C、120°和60°是补角 D、60°是30°的补角9. 把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、D、B三点在同一直线上,BM为∠ABC的平分线,BN为∠CBE的平分线,则∠MBN的度数是( )
A、圆柱 B、圆锥 C、球 D、棱柱7. 用一副三角板不能画出( )A、75°角 B、135°角 C、160°角 D、105°角8. 下列叙述正确的是( )A、180°是补角 B、120°和60°互为补角 C、120°和60°是补角 D、60°是30°的补角9. 把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、D、B三点在同一直线上,BM为∠ABC的平分线,BN为∠CBE的平分线,则∠MBN的度数是( ) A、30° B、45° C、55° D、60°10. 如图,长度为18cm的线段AB的中点为M,点C是线段MB的一个三等分点,则线段AC的长为( )
A、30° B、45° C、55° D、60°10. 如图,长度为18cm的线段AB的中点为M,点C是线段MB的一个三等分点,则线段AC的长为( ) A、12cm B、6cm C、9cm D、3cm11. 如图,∠AOB为平角,且∠AOC= ∠BOC,则∠BOC的度数是( )
A、12cm B、6cm C、9cm D、3cm11. 如图,∠AOB为平角,且∠AOC= ∠BOC,则∠BOC的度数是( ) A、140° B、135° C、120° D、40°12. 已知在线段上依次添加1个点,2个点,3个点,……,原线段上所成线段的总条数如下表:
A、140° B、135° C、120° D、40°12. 已知在线段上依次添加1个点,2个点,3个点,……,原线段上所成线段的总条数如下表:添加点数
1
2
3
4
线段总条数
3
6
10
15
若在原线段上添加n个点,则原线段上所有线段总条数为( )
A、n+2 B、1+2+3+…+n+n+1 C、n+1 D、二、填空题
-
13. 已知∠1=20°,∠2=30°,∠3=60°,∠4=150°,则∠2是的余角,是∠4的补角.
14. 如图,将三个同样的正方形的一个顶点重合放置,那么∠1的度数为 . 15. 已知A、B、C三点都在数轴上,点A在数轴上对应的数为2,且AB=5,BC=3,则点C在数轴上对应的数为 .16. 如图,点A,B,C在直线l上,则图中共有条线段,有条射线.
15. 已知A、B、C三点都在数轴上,点A在数轴上对应的数为2,且AB=5,BC=3,则点C在数轴上对应的数为 .16. 如图,点A,B,C在直线l上,则图中共有条线段,有条射线.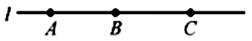 17. 如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOD=120°,则∠DOE= , ∠COE= .
17. 如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOD=120°,则∠DOE= , ∠COE= . 18. 用棱长是1cm的小正方体组成如图所示的几何体,把这个几何体放在桌子上,并把暴露的面涂上颜色,那么涂颜色面的面积之和是cm2.
18. 用棱长是1cm的小正方体组成如图所示的几何体,把这个几何体放在桌子上,并把暴露的面涂上颜色,那么涂颜色面的面积之和是cm2.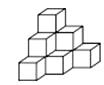
三、解答题
-
19. 已知:如图,线段 , ;请按下列步骤画图:(用圆规和直尺画图,不写画法、保留作图痕迹)

①画线段BC,使得BC= ;
②在直线BC外任取一点A,画直线AB和射线AC.
20. 一个角的余角比它的补角的 还少40°,求这个角。21. 已知线段AB=20cm,M是线段AB的中点,C是线段AB延长线上的点,AC:BC=3:1,点D是线段BA延长线上的点,AD=AB.求:(1)、线段BC的长;(2)、线段MD的长.22. 如图,点O是射线OC与直线AB的交点.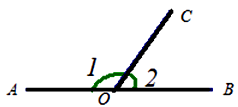 (1)、若∠1=120°,求∠2的度数;(2)、若已知∠1的一半比∠2小30°,求∠1和∠2的度数.23. 如图
(1)、若∠1=120°,求∠2的度数;(2)、若已知∠1的一半比∠2小30°,求∠1和∠2的度数.23. 如图
 (1)、如图1,已知点D是线段AC的中点,点B在线段DC上,且AB=4BC,若BD=6 cm,求AB的长;
(1)、如图1,已知点D是线段AC的中点,点B在线段DC上,且AB=4BC,若BD=6 cm,求AB的长;
(2)、如图2,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE,试求∠COE的度数.24. 如图,甲、乙两船同时从小岛A出发,甲船沿北偏西20°的方向以40海里/时的速度航行;乙船沿南偏西80°的方向以30海里/时的速度航行.半小时后,两船分别到达B,C两处. (1)、以1cm表示10海里,在图中画出B,C的位置;(2)、求A处看B,C两处的张角∠BAC的度数;(3)、测出B,C两处的图距,并换算成实际距离(精确到1海里).25. 如图,P是线段AB上任一点,AB=12 cm,C、D两点分别从P、B同时向A点运动,且C点的运动速度为2 cm/s,D点的运动速度为3 cm/s,运动的时间为t s.
(1)、以1cm表示10海里,在图中画出B,C的位置;(2)、求A处看B,C两处的张角∠BAC的度数;(3)、测出B,C两处的图距,并换算成实际距离(精确到1海里).25. 如图,P是线段AB上任一点,AB=12 cm,C、D两点分别从P、B同时向A点运动,且C点的运动速度为2 cm/s,D点的运动速度为3 cm/s,运动的时间为t s. (1)、若AP=8 cm.
(1)、若AP=8 cm.①运动1s后,求CD的长;
②当D在线段PB运动上时,试说明AC=2CD;
(2)、如果t=2 s时,CD=1 cm,试探索AP的值.26. 定义:从一个角的顶点出发,把这个角分成1∶2的两个角的射线,叫作这个角的三分线,显然,一个角的三分线有两条.例如:如图①,若∠BOC=2∠AOC,则OC是∠AOB的一条三分线.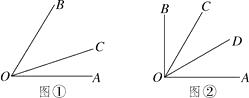 (1)、已知:如图①,OC是∠AOB的一条三分线,且∠BOC>∠AOC,若∠AOB=60°,求∠AOC的度数;(2)、已知:∠AOB=90°,如图②,若OC,OD是∠AOB的两条三分线.
(1)、已知:如图①,OC是∠AOB的一条三分线,且∠BOC>∠AOC,若∠AOB=60°,求∠AOC的度数;(2)、已知:∠AOB=90°,如图②,若OC,OD是∠AOB的两条三分线.①求∠COD的度数;
②现以O为中心,将∠COD顺时针旋转n度得到∠C′OD′,当OA恰好是∠C′OD′的三分线时,求n的值.