人教版七年级数学上册 第三章一元一次方程 单元检测b卷

试卷更新日期：2018-10-24 类型：单元试卷

进入 出卷网 下载

一、选择题

  • 1. 已知方程x2k﹣1+k=0是关于x的一元一次方程，则方程的解等于（   ）
    A、﹣1 B、1 C、12 D、﹣ 12

    查看试题解析

  • 2. 若x=1是方程（1）2﹣ 13(m−x)=2x 的解，则关于y的方程（2）m（y﹣3）﹣2=m（2y﹣5）的解是（    ）
    A、﹣10 B、0 C、43 D、4

    查看试题解析

  • 3. 如果x=﹣1是关于x的方程x+2k﹣3=0的解，则k的值是（    ）
    A、﹣1 B、1 C、﹣2 D、2

    查看试题解析

  • 4. 阅读：关于x方程ax=b在不同的条件下解的情况如下：（1）当a≠0时，有唯一解x= ba ；（2）当a=0，b=0时有无数解；（3）当a=0，b≠0时无解．请你根据以上知识作答：已知关于x的方程 x3 •a= x2 ﹣ 16 （x﹣6）无解，则a的值是（   ）
    A、1 B、﹣1 C、±1 D、a≠1

    查看试题解析

  • 5. 如图，六位朋友均匀的围坐在圆桌旁聚会．圆桌的半径为80cm，每人离桌边10cm，又后来两位客人，每人向后挪动了相同距离并左右调整位置，使8个人都坐下，每相邻两人之间的距离与原来相邻两人之间的距离（即在圆周上两人之间的圆弧的长）相等．设每人向后挪动的距离为xcm．则根据题意，可列方程为（    ）

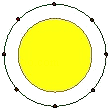    A、60π(80+10)180=45π(80+10+x)180 B、45π×80180=36π(80+x)180 C、2π（80+10）×8=2π（80+x）×10 D、2π（80﹣x）×10=2π（80+x）×8

    查看试题解析

  • 6. 桌面上有甲、乙、丙三个圆柱形的杯子，杯深均为15公分，各装有10公分高的水，且表记录了甲、乙、丙三个杯子的底面积．今小明将甲、乙两杯内一些水倒入丙杯，过程中水没溢出，使得甲、乙、丙三杯内水的高度比变为3：4：5．若不计杯子厚度，则甲杯内水的高度变为多少公分？（    ）


    底面积（平方公分）

    甲杯

    60

    乙杯

    80

    丙杯

    100

    A、5.4 B、5.7 C、7.2 D、7.5

    查看试题解析

  • 7. 已知关于x的方程2x﹣3= m3 +x的解满足|x|=1，则m的值是（    ）
    A、﹣6 B、﹣12 C、﹣6或﹣12 D、6或12

    查看试题解析

  • 8. 某企业接到为地震灾区生产活动房的任务，此企业拥有九个生产车间，现在每个车间原有的成品活动房一样多，每个车间的生产能力也一样．有A、B两组检验员，其中A组有8名检验员前两天时间将第一、二车间的所有成品（原来的和这两天生产的）检验完毕后，再去检验第三、四车间所有成品，又用去三天时间；同时这五天时间B组检验员也检验完余下的五个车间的所有成品．如果每个检验员的检验速度一样快，那么B组检验员人数为（    ）
    A、8人 B、10人 C、12人 D、14人

    查看试题解析

  • 9. 若x+3y=5，则代数式2x+6y﹣3的值是（    ）
    A、9 B、10 C、7 D、15

    查看试题解析

  • 10. 小明今年12岁，他爷爷60岁，经过（   ）年以后，爷爷的年龄是小明的4倍．
    A、2 B、4 C、6 D、8

    查看试题解析

二、填空题

  • 11. 小明解方程 2x−13 = x+a2 ﹣3去分母时，方程右边的﹣3忘记乘6，因而求出的解为x=2，则原方程正确的解为 ．

    查看试题解析

  • 12. 方程 x2+m3=x−4 与方程1=x+7的解相同，则m的值为 ．

    查看试题解析

  • 13. 已知x=﹣2是方程20x+|k﹣1|=﹣40的解，则k的值是 ．

    查看试题解析

  • 14. 已知关于x的方程2ax =(a+1)x+3的解是正整数，则正整数a =.

    查看试题解析

  • 15. 若x=0是方程2017x﹣a=2018x+4的解，则代数式﹣a2﹣a+2的值为 ．

    查看试题解析

  • 16. 请将下面的同类项用连线连接起来：

    查看试题解析

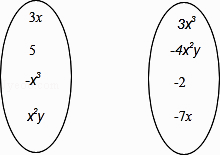  • 17. 若关于x的方程2x﹣a=0与2x+3a﹣16=0的解相同，则这两个方程的解为x= ．

    查看试题解析

  • 18. 若a、b互为相反数，c、d互为倒数，p的绝对值等于2，则关于x的方程（a+b）x+3cdx+p=0的解为 ．

    查看试题解析

  • 19. 如图是2005年5月份的日历，如图中那样，用一个圈竖着圈住3个数，如果被圈住的三个数的和为30，则这三个数最小一个所表示的日期为2005年5月日．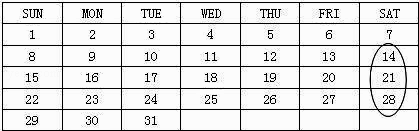

    查看试题解析

三、解答题

  • 20. 解方程  
    (1)、5x+3（2﹣x）=8
    (2)、x−32 ﹣ 4x+15 =1．

    查看试题解析

  • 21. 某中学组织七年级学生参观，原计划租用45座客车若干辆，但有15人没有座位；如果租用同样数量的60座客车，则多出一辆，且其余客车恰好坐满．试问：
    (1)、七年级学生人数是多少？
    (2)、原计划租用45座客车多少辆？

    查看试题解析

  • 22. 列方程解应用题：  
    (1)、一个箱子，如果装橙子可以装18个，如果装梨可以装16个，现共有橙子、梨400个，而且装梨的箱子是装橙子箱子的2倍．请算一下，装橙子和装梨的箱子各多少个？
    (2)、一群小孩分一堆苹果，每人3个多7个，每人4个少3个，求有几个小孩？几个苹果？
    (3)、一架飞机在两城之间飞行，风速为24千米/时．顺风飞行需要2小时50分，逆风飞行需要3小时，求无风时飞机的速度和两城之间的航程．

    查看试题解析

  • 23. 下表为某市居民每月用水收费标准．（单位：元/m3）．

    用水量

    单价

    x≤22

    a

    超出部分

    a+1.1

    (1)、某用户用水10立方米，共交水费23元，求a的值；
    (2)、在（1）的前提下，该用户5月份交水费71元，请问该用户用水多少立方米？（请列方程解答）

    查看试题解析

  • 24.   
    (1)、若|x+5|=2，则x=；
    (2)、代数式|x﹣1|+|x+3|的最小值为 ， 当取此最小值时，x的取值范围是；
    (3)、解方程：|2x+4|﹣|x﹣3|=9．

    查看试题解析

  • 25. 一个自行车队进行训练，训练时所有队员都以35千米/时的速度前进，突然一号队员以45千米/时的速度独自行进10千米后掉转车头，仍以45千米/时的速度往回骑，直到与其他队员会合，一号队员从离队开始到与队员重新会合，经过了多长时间？

    查看试题解析

  • 26. 甲、乙两支“徒步队”到野外沿相同路线徒步，徒步的路程为24千米．甲队步行速度为4千米/时，乙队步行速度为6千米/时．甲队出发1小时后，乙队才出发，同时乙队派一名联络员跑步在两队之间来回进行一次联络（不停顿），他跑步的速度为10千米/时．
    (1)、乙队追上甲队需要多长时间？
    (2)、联络员从出发到与甲队联系上后返回乙队时，他跑步的总路程是多少？
    (3)、从甲队出发开始到乙队完成徒步路程时止，何时两队间间隔的路程为1千米？

    查看试题解析

  • 27. 某城市对用户的自来水收费实行阶梯水价，收费标准如下表所示：

    月用水量

    不超过12吨的部分

    超过12吨不超过18吨的部分

    超过18吨的部分

    收费标准（元/吨）

    2.00

    2.50

    3.00

    (1)、某用户5月份缴水费45元，则该用户5月份的用水量是多少？
    (2)、某用户想月所缴水费控制在20元至30元之间，则该用户的月用水量应该如何控制？
    (3)、若某用户的月用水量为m吨，请用含m的代数式表示该用户月所缴水费．

    查看试题解析

  • 28. 学校有6名教师和234名学生集体外出活动，准备租用45座大客车和30座小客车．若租用1辆大客车和2辆小客车共需租车费1000元；若租用2辆大客车和1辆小客车共需租车费1100元．
    (1)、求大、小客车每辆的租车费各是多少元？
    (2)、若要保证每位师生都有座位，每辆车上恰好分配1名教师，共有几种租车方案，各种方案需租车费多少元．

    查看试题解析