人教版七年级数学上册第一章有理数单元检测c卷

试卷更新日期：2018-10-24 类型：单元试卷

进入出卷网下载

一、选择题

1. 6的相反数为（）

A、﹣6 B、6 C、﹣ $\frac{1}{6}$ D、 $\frac{1}{6}$

查看试题解析
2. 据资料显示，地球的海洋面积约为360000000平方千米，请用科学记数法表示地球海洋面积面积约为多少平方千米（）

A、36×10⁷ B、3.6×10⁸ C、0.36×10⁹ D、3.6×10⁹

查看试题解析
3. 如图，点A所表示的数的绝对值是（）

A、3 B、﹣3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
4. 近似数35.04万精确到（）

A、百位 B、百分位 C、万位 D、个位

查看试题解析
5. 如图，在一个由6个圆圈组成的三角形里，把1到6这6个数分别填入图的圆圈中，要求三角形的每条边上的三个数的和S都相等，那么S的最大值是（）

A、9 B、10 C、12 D、13

查看试题解析
6. 关于﹣（﹣a）²的相反数，有下列说法：①等于a²；②等于（﹣a）²；③值可能为0；④值一定是正数．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 10个互不相等的有理数，每9个的和都是“分母为22的既约真分数（分子与分母无公约数的真分数）”，则这10个有理数的和为（）

A、 $\frac{1}{2}$ B、 $\frac{11}{18}$ C、 $\frac{7}{6}$ D、 $\frac{5}{9}$

查看试题解析
8. 取一个自然数，若它是奇数，则乘以3加上1，若它是偶数，则除以2，按此规则经过若干步的计算最终可得到1．这个结论在数学上还没有得到证明．但举例验证都是正确的．例如：取自然数5．经过下面5步运算可得1，即：如图所示．如果自然数m恰好经过7步运算可得到1，则所有符合条件的m的值有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
9. 如图，现有3×3的方格，每个小方格内均有不同的数字，要求方格内每一行．每一列以及每一条对角线上的三个数字之和均相等，图中给出了部分数字，则P处对应的数字是（）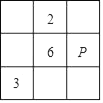

A、7 B、5 C、4 D、1

查看试题解析

二、填空题

10. 如果水位升高2m时，水位的变化记为+2m，那么水位下降3m时，水位的变化情况是．

查看试题解析
11. 根据滨湖区旅游局数据统计显示，今年“五一”小长假，鼋头渚、灵山圣境、三国水浒城三大5A景区共接待旅游总人数254000人，这个数据用科学记数法可表示为人．

查看试题解析
12. 定义运算“*”，规定x*y=2x+y，如1*2=4，2*3=7，则（﹣2）*5= ．

查看试题解析
13. 下面是一种算法：输入任意一个数x，都是“先乘以2，再减去3”，进行第1次这样的运算，结果为y₁ ，再对y₁实施同样的运算，称为第2次运算，结果为y₂ ，这样持续进行，要使第n次运算结果为0，即y_n=0，则最初输入的数应该是．（用含有n的代数式表示）．

查看试题解析
14. 阅读材料：若a^b=N，则b=log_aN，称b为以a为底N的对数，例如2³=8，则log₂8=log₂2³=3．根据材料填空：log₃9= ．

查看试题解析
15. 某公园划船项目收费标准如下：
船型
两人船
（限乘两人）
四人船
（限乘四人）
六人船
（限乘六人）
八人船
（限乘八人）
每船租金
（元/小时）
90
100
130
150
某班18名同学一起去该公园划船，若每人划船的时间均为1小时，则租船的总费用最低为元．

查看试题解析
16. 如图，程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”，执行程序框图，如果输入a，b的值分别为3，9，那么输出a的值为．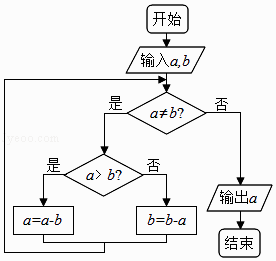

查看试题解析
17. 【阅读材料】“九宫图”源于我国古代夏禹时期的“洛书”（图1所示），是世界上最早的矩阵，又称“幻方”，用今天的数学符号翻译出来，“洛书”就是一个三阶“幻方”（图2所示）．
【规律总结】观察图1、图2，根据“九宫图”中各数字之间的关系，我们可以总结出“幻方”需要满足的条件是；若图3，是一个“幻方”，则a= ．

查看试题解析

三、解答题

18. 计算：﹣2³+6÷3× $\frac{2}{3}$
圆圆同学的计算过程如下：
原式=﹣6+6÷2=0÷2=0
请你判断圆圆的计算过程是否正确，若不正确，请你写出正确的计算过程．

查看试题解析
19. 计算：|4﹣4 $\frac{1}{2}$ |+（ $- \frac{1}{2} + \frac{2}{3} - \frac{1}{6}$ ） $\div \frac{1}{12} - 2^{2}$ ﹣（+5）．

查看试题解析
20. 对于有理数a、b，定义一种新运算“⊙”，规定：a⊙b=|a+b|+|a﹣b|．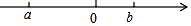

(1)、计算2⊙（﹣4）的值；

(2)、若a，b在数轴上的位置如图所示，化简a⊙b．

查看试题解析
21. 【概念学习】
规定：求若干个相同的有理数（均不等于0）的除法运算叫做除方，如2÷2÷2，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）等．类比有理数的乘方，我们把2÷2÷2记作2^③ ，读作“2的圈3次方”，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）记作（﹣3）^④ ，读作“﹣3的圈4次方”，一般地，把 $\underset{n 个 a}{\underset{︸}{a \div a \div a \div \dots \div a}}$ （a≠0）记作a^ⓝ ，读作“a的圈 n次方”．

(1)、【初步探究】
Ⅰ.直接写出计算结果：2^③= ▲ ，（﹣ $\frac{1}{2}$ ）^⑤= ▲ ；
Ⅱ.关于除方，下列说法错误的是 ▲
A．任何非零数的圈2次方都等于1；
B．对于任何正整数n，1^ⓝ=1；
C.3^④=4^③；
D．负数的圈奇数次方结果是负数，负数的圈偶数次方结果是正数．

(2)、【深入思考】
我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘方运算呢？
Ⅰ.试一试：仿照上面的算式，将下列运算结果直接写成幂的形式．
（﹣3）^④= ▲ ； 5^⑥= ▲ ；（﹣ $\frac{1}{2}$ ）^⑩= ▲ ．
Ⅱ.想一想：将一个非零有理数a的圈n次方写成幂的形式等于 ▲ ；
Ⅲ.算一算：12²÷（﹣ $\frac{1}{3}$ ）^④×（﹣2）^⑤﹣（﹣ $\frac{1}{3}$ ）^⑥÷3³ ．

查看试题解析
22. 如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动，它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负．例如从A到B记为：A→B（+1，+4），从D到C记为：D→C（﹣1，+2），其中第一个数表示左右方向，第二个数表示上下方向．

(1)、图中A→C（，），B→C（，），D→（﹣4，﹣2）；

(2)、若这只甲虫从A处去P处的行走路线依次为（+2，+2），（+2，﹣1），（﹣2，+3），（﹣1，﹣2），请在图中标出P的位置；

(3)、若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程．

查看试题解析
23. 【新知理解】
如图①，点C在线段AB上，若BC=πAC，则称点C是线段AB的圆周率点，线段AC、BC称作互为圆周率伴侣线段．

(1)、若AC=3，则AB=；

(2)、若点D也是图①中线段AB的圆周率点（不同于点C），则ACBD；（填“=”或“≠”）

(3)、【解决问题】
如图②，现有一个直径为1个单位长度的圆片，将圆片上的某点与数轴上表示1的点重合，并把圆片沿数轴向右无滑动地滚动1周，该点到达点C的位置．
若点M、N是线段OC的圆周率点，求MN的长；

(4)、图②中，若点D在射线OC上，且线段CD与以O、C、D中某两个点为端点的线段互为圆周率伴侣线段，请直接写出点D所表示的数．

查看试题解析

人教版七年级数学上册 第一章有理数 单元检测c卷

一、选择题

二、填空题

三、解答题

人教版七年级数学上册第一章有理数单元检测c卷