广东省广州市天河区2018届九年级数学中考一模试卷

试卷更新日期：2018-10-24 类型：中考模拟

进入出卷网下载

一、单选题

1. 3的相反数是（）

A、 $\frac{1}{3}$ B、- $\frac{1}{3}$ C、3 D、﹣3

查看试题解析
2. 如图所示的几何体是由四个完全相同的正方体组成的，这个几何体的俯视图是（）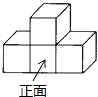

A、 B、 C、 D、

查看试题解析
3. 下面的运算正确的是（）

A、a+a²=a³ B、a²•a³=a⁵ C、6a﹣5a=1 D、a⁶÷a²=a³

查看试题解析
4. 下列图形中，不是中心对称图形有（）

A、 B、 C、 D、

查看试题解析
5. 在平面直角坐标系中，二次函数y=2（x﹣1）²+3的顶点坐标是（）

A、（1，3） B、（1，﹣3） C、（﹣1，3） D、（﹣1，﹣3）

查看试题解析
6. 若y＝kx－4的函数值y随x的增大而增大，则k的值可能是下列的（）

A、－2 B、－ $\frac{1}{2}$ C、0 D、2

查看试题解析
7. 如图，△ABC中，∠C=90°，AC=16cm，AB的中垂线MN交AC于点D，连接BD，若cos∠BDC= $\frac{3}{5}$ ，则BC=（）

A、8cm B、4cm C、6cm D、10cm

查看试题解析
8. 祁中初三66班学生毕业时，每个同学都要给其他同学写一份毕业留言作为纪念，全班学生共写了930份留言．如果全班有x名学生，根据题意，列出方程为（）

A、 $\frac{x (x - 1)}{2}$ =930 B、 $\frac{x (x + 1)}{2}$ =930 C、x（x+1）=930 D、x（x﹣1）=930

查看试题解析
9. 如图，PA和PB是⊙O的切线，点A和B的切点，AC是⊙O的直径，已知∠P=50°，则∠ACB的大小是（）

A、65° B、60° C、55° D、50°

查看试题解析
10. 如图，菱形ABCD中，AB=AC，点E、F分别为边AB、BC上的点，且AE=BF，连接CE、AF交于点H，则下列结论：①△ABF≌△CAE；②∠AHC=120°；③△AEH∽△CEA；④AE•AD=AH•AF；其中结论正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 如图，已知正方形ABCD边长为3，点E在AB边上且BE=1，点P，Q分别是边BC，CD的动点（均不与顶点重合），当四边形AEPQ的周长取最小值时，四边形AEPQ的面积是（）

A、3 B、5 C、4.5 D、1

查看试题解析

二、填空题

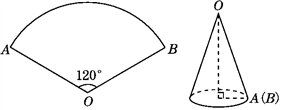
12. 分解因式：x²＋3x＝.

查看试题解析
13. 在函数 $y = \sqrt{2 x - 1}$ 中，自变量 $x$ 的取值范围是．

查看试题解析
14. 把103000000这个数用科学记数法表示为．

查看试题解析
15. 若a、b、c为三角形的三边，且a、b满足 $\sqrt{a^{2} -6a+ 9} + {(b - 2)}^{2} = 0$ ，则第三边c的取值范围是．

查看试题解析
16. 如图，用一个圆心角为120°的扇形围成一个无底的圆锥，如果这个圆锥底面圆的半径为1 cm，则这个扇形的半径是cm.

查看试题解析

三、解答题

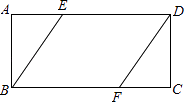
17. 解方程组： ${\begin{array}{l} \end{array} \begin{matrix} x + 2 y = 1 \\ 3 x - 2 y = 11 \end{matrix}$ .

查看试题解析
18. 已知，如图，E、F分别为矩形ABCD的边AD和BC上的点，AE=CF．求证：BE=DF．

查看试题解析
19. 先化简，再求值： $\frac{x}{x^{2} - 1}$ ÷（1+ $\frac{1}{x - 1}$ ），其中x= $\sqrt{2}$ ﹣1．

查看试题解析
20. 为了解今年初三学生的数学学习情况，某校对上学期的数学成绩作了统计分析，绘制得到如下图表．请结合图表所给出的信息解答下列问题：
成绩
频数
频率
优秀
45
b
良好
a
0.3
合格
105
0.35
不合格
60
c

(1)、该校初三学生共有多少人？

(2)、求表中a，b，c的值，并补全条形统计图．

(3)、初三（一）班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍，求恰好选中甲、乙两位同学的概率．

查看试题解析
21. 如图，在平行四边形ABCD中，AB＜BC．

(1)、利用尺规作图，在BC边上确定点E，使点E到边AB，AD的距离相等（不写作法，保留作图痕迹）；

(2)、若BC=8，CD=5，则CE= ．

查看试题解析
22. 始兴县太平镇2012年有绿地面积57.5公顷，该镇近几年不断增加绿地面积，2014年达到82.8公顷．

(1)、求该镇2012至2014年绿地面积的年平均增长率；

(2)、若年增长率保持不变，2015年该镇绿地面积能否达到100公顷？

查看试题解析
23. 如图，直线y=2x与反比例函数y= $\frac{k}{x}$ （k≠0，x＞0）的图象交于点A（1，a），B是反比例函数图象上一点，直线OB与x轴的夹角为α，tanα= $\frac{1}{2}$ ．

(1)、求k的值及点B坐标．

(2)、连接AB，求三角形AOB的面积S_△AOB ．

查看试题解析
24. 如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作⊙O的切线DF，交AC于点F．

(1)、求证：DF⊥AC；

(2)、若⊙O的半径为4，∠CDF=22.5°，求阴影部分的面积．

查看试题解析
25. 如图，在平面直角坐标系xOy中，二次函数y=ax²+bx﹣4（a≠0）的图象与x轴交于A（﹣2，0）、C（8，0）两点，与y轴交于点B，其对称轴与x轴交于点D．

(1)、求该二次函数的解析式；

(2)、如图1，连结BC，在线段BC上是否存在点E，使得△CDE为等腰三角形？若存在，求出所有符合条件的点E的坐标；若不存在，请说明理由；

(3)、如图2，若点P（m，n）是该二次函数图象上的一个动点（其中m＞0，n＜0），连结PB，PD，BD，求△BDP面积的最大值及此时点P的坐标．

查看试题解析

成绩	频数	频率
优秀	45	b
良好	a	0.3
合格	105	0.35
不合格	60	c