广东省东莞市中堂镇六校2018届数学中考三模试卷
试卷更新日期:2018-10-24 类型:中考模拟
一、单选题
-
1. 截止到2015年6月1日,北京市已建成34个地下调蓄设施,蓄水能力达到140000立方米,将140000用科学记数法表示应为( )A、14×104 B、1.4×105 C、1.4×106 D、14×1062. 若数轴上表示﹣1和3的两点分别是点A和点B,则点A和点B之间的距离是( )A、﹣4 B、﹣2 C、2 D、43. 一个不透明的盒子中装有3个红球,2个黄球和1个绿球,这些球除了颜色外无其他差别,从中随机摸出一个小球,恰好是黄球的概率为( )A、 B、 C、 D、4. 6的倒数是( )A、 B、- C、6 D、﹣65. 观察下列图形,其中既是轴对称又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 6. 如图,直线l1 , l2 , l3交于一点,直线l4∥l1 , 若∠1=124°,∠2=88°,则∠3的度数为( )
6. 如图,直线l1 , l2 , l3交于一点,直线l4∥l1 , 若∠1=124°,∠2=88°,则∠3的度数为( )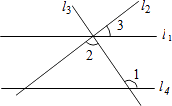 A、26° B、36° C、46° D、56°7. 一元二次方程x2﹣7x﹣2=0的实数根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定8. 下列哪一个是假命题( )A、五边形外角和为360° B、切线垂直于经过切点的半径 C、(3,﹣2)关于y轴的对称点为(﹣3,2) D、抛物线y=x2﹣4x+2017对称轴为直线x=29. 一元一次不等式组 的解集在数轴上表示出来,正确的是( )A、
A、26° B、36° C、46° D、56°7. 一元二次方程x2﹣7x﹣2=0的实数根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定8. 下列哪一个是假命题( )A、五边形外角和为360° B、切线垂直于经过切点的半径 C、(3,﹣2)关于y轴的对称点为(﹣3,2) D、抛物线y=x2﹣4x+2017对称轴为直线x=29. 一元一次不等式组 的解集在数轴上表示出来,正确的是( )A、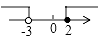 B、
B、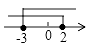 C、
C、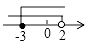 D、
D、 10. 如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是( )
10. 如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是( )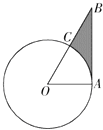 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
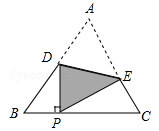
11. 已知∠A=40°,则∠A的余角的度数是12. 计算:m3÷m2= .13. 在平面直角坐标系中有一点A(﹣2,1),将点A先向右平移3个单位,再向下平移2个单位,则平移后点A的坐标为 .14. 观察下列单项式:a,-2a2 , 4a3 , -8a4 , 16a5 , ….按此规律,第7个单项式是 .15. 如图,把等边△ABC沿着DE折叠,使点A恰好落在BC边上的点P处,且DP⊥BC,若BP=4cm,则EC=cm.
三、解答题
-
16. 计算:|-2|+ -(-1)2 .17. 先化简,再求值: ,其中x=﹣1.18. 如图,在Rt△ABC中,∠C=90°.作∠BAC的平分线AP交边BC于点D. (保留作图痕迹,不写作法);若∠BAC=28°,求∠ADB的度数.
 19. 车辆经过润扬大桥收费站时,4个收费通道A、B、C、D中,可随机选择其中的一个通过.(1)、一辆车经过此收费站时,选择A通道通过的概率是;(2)、求两辆车经过此收费站时,选择不同通道通过的概率(请用树状图或列表法等方式给出分析过程).20. 学校准备购进一批篮球和足球,买1个篮球和2个足球共需170元,买2个篮球和1个足球共需190元.(1)、求一个篮球和一个足球的售价各是多少元?(2)、学校欲购进篮球和足球共100个,且足球数量不多于篮球数量的2倍,求出最多购买足球多少个?21. 在▱ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
19. 车辆经过润扬大桥收费站时,4个收费通道A、B、C、D中,可随机选择其中的一个通过.(1)、一辆车经过此收费站时,选择A通道通过的概率是;(2)、求两辆车经过此收费站时,选择不同通道通过的概率(请用树状图或列表法等方式给出分析过程).20. 学校准备购进一批篮球和足球,买1个篮球和2个足球共需170元,买2个篮球和1个足球共需190元.(1)、求一个篮球和一个足球的售价各是多少元?(2)、学校欲购进篮球和足球共100个,且足球数量不多于篮球数量的2倍,求出最多购买足球多少个?21. 在▱ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.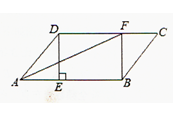 (1)、求证:四边形BFDE是矩形;(2)、若AF平分∠BAD,且AE=3,DE=4,求tan∠BAF的值.22. 已知抛物线y= x2+1(如图所示).
(1)、求证:四边形BFDE是矩形;(2)、若AF平分∠BAD,且AE=3,DE=4,求tan∠BAF的值.22. 已知抛物线y= x2+1(如图所示).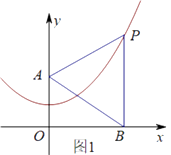 (1)、填空:抛物线的顶点坐标是( , ),对称轴是;(2)、如图1,已知y轴上一点A(0,2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若△PAB是等边三角形,求点P的坐标;(3)、如图,在第二问的基础上,在抛物线上有一点C(x,y),连接AC、OC、BC、PC,当△OAC的面积等于△BCP的面积时,求C的横坐标.23. 如图,四边形ABCD内接于⊙O,AB=AD,对角线BD为⊙O的直径,AC与BD交于点E.点F为CD延长线上,且DF=BC.
(1)、填空:抛物线的顶点坐标是( , ),对称轴是;(2)、如图1,已知y轴上一点A(0,2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若△PAB是等边三角形,求点P的坐标;(3)、如图,在第二问的基础上,在抛物线上有一点C(x,y),连接AC、OC、BC、PC,当△OAC的面积等于△BCP的面积时,求C的横坐标.23. 如图,四边形ABCD内接于⊙O,AB=AD,对角线BD为⊙O的直径,AC与BD交于点E.点F为CD延长线上,且DF=BC.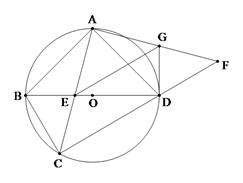 (1)、证明:AC=AF;(2)、若AD=2,AF= ,求AE的长;(3)、若EG∥CF交AF于点G,连接DG.证明:DG为⊙O的切线.24. 两个等腰直角三角形如图放置,∠B=∠CAD=90°,AB=BC= cm,AC=AD,垂直于CD的直线a从点C出发,以每秒 cm的速度沿CD方向匀速平移,与CD交于点E,与折线BAD交于点F;与此同时,点G从点D出发,以每秒1cm的速度沿着DA的方向运动;当点G落在直线a上,点G与直线a同时停止运动;设运动时间为t秒(t>0).
(1)、证明:AC=AF;(2)、若AD=2,AF= ,求AE的长;(3)、若EG∥CF交AF于点G,连接DG.证明:DG为⊙O的切线.24. 两个等腰直角三角形如图放置,∠B=∠CAD=90°,AB=BC= cm,AC=AD,垂直于CD的直线a从点C出发,以每秒 cm的速度沿CD方向匀速平移,与CD交于点E,与折线BAD交于点F;与此同时,点G从点D出发,以每秒1cm的速度沿着DA的方向运动;当点G落在直线a上,点G与直线a同时停止运动;设运动时间为t秒(t>0).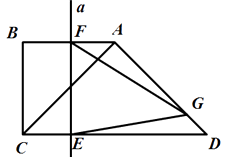

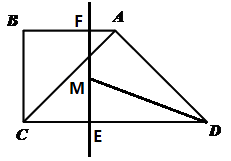 (1)、填空:CD=cm;(2)、连接EG、FG,设△EFG的面积为y,求y与t之间的函数关系式,并写出相应t的取值范围;(3)、是否存在某一时刻t(0<t<2),作∠ADC的平分线DM交EF于点M,是否存在点M是EF的中点?若存在,求此时的t值;若不存在,请说明理由。
(1)、填空:CD=cm;(2)、连接EG、FG,设△EFG的面积为y,求y与t之间的函数关系式,并写出相应t的取值范围;(3)、是否存在某一时刻t(0<t<2),作∠ADC的平分线DM交EF于点M,是否存在点M是EF的中点?若存在,求此时的t值;若不存在,请说明理由。