湘教版七年级数学上册 第四章图形的认识 单元检测b卷
试卷更新日期：2018-10-22 类型：单元试卷
一、选择题
-
1.
下面的几何体中，属于棱柱的有（ ）
A、1个 B、2个 C、3个 D、4个2. 如图，直线AB和CD相交于点O，若∠AOD与∠BOC的和为236°，则∠AOC的度数为（ ）
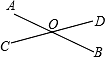A、62° B、118° C、72° D、59°3. 如图给定的是纸盒的外表面，下面能由它折叠而成的是（ ）
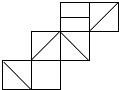A、
B、
C、
D、
4. 某校七年级在下午3：00开展“阳光体育”活动．下午3：00这一时刻，时钟上分针与时针所夹的角等于（ ）A、30° B、60° C、90° D、120°5. 下列说法中正确的个数为（ ）①过两点有且只有一条直线；
②连接两点的线段叫两点间的距离；
③两点之间所有连线中，线段最短；
④射线比直线小一半．
A、1个 B、2个 C、3个 D、4个6. 如图所示，用量角器度量∠AOB，可以读出∠AOB的度数为（ ）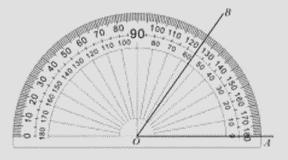
A、45° B、55° C、125° D、135°7. 下列结论中，不正确的是（ ）A、两点确定一条直线 B、两点之间，直线最短 C、等角的余角相等 D、等角的补角相等8. 平面上有三个点，可以确定直线的条数是 （ ）A、1条 B、2条 C、3条 D、1条或3条9.某公司员工分别在A、B、C三个住宅区，A区有30人，B区有30人，C区有10人，三个区在同一条直线上，如图所示，该公司的接送车打算在此间只设一个停靠点，为使所有员工步行到停靠点的路程之和最小，那么停靠点的位置应设在（ ）
A、A区 B、B区 C、C区 D、A、B两区之间10. 已知∠AOB=3∠BOC，若∠BOC=30°，则∠AOC等于（ ）A、120° B、120°或60° C、30° D、30°或90°11. 已知线段AB=6cm，若M是AB的三等分点，N是AM的中点，则线段MN的长度为（ ）A、1cm B、2cm C、1.5cm D、1cm或2cm12. 挑游戏棒是一种好玩的游戏，游戏规则：当一根棒条没有被其它棒条压着时，就可以把它往上拿走。如图中，按照这一规则，第1次应拿走⑨号棒，第2次应拿走⑤号棒，…，则第6次应拿走（ ）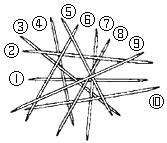
A、②号棒 B、⑦号棒 C、⑧号棒 D、⑩号棒二、填空题
-
13. 如图，已知线段AC，点D为AC的中点，BC= AB，BD=1cm，则AC= ．
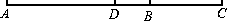14. 如图所示，点O是直线AB上的点，OC平分∠AOD，∠BOD=40°，则∠AOC=°．
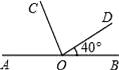15. 要把一根木条在墙上钉牢，至少需要枚钉子．其中的道理是16. 一个正方体的六个面上分别涂有红、白、黄、绿、蓝、紫六种不同的颜色，其中红、白、黄、绿、蓝、紫，分别代表的是数字﹣1、﹣2、﹣3、﹣4、﹣5、﹣6中的一个数，如图是这个正方体的三种放置方法，若三个正方体下底面所标颜色代表的数字分别是a，b，c，则a+b+c+abc= ．
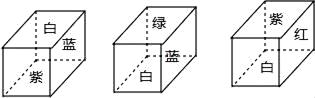17. 如图，已知点C在线段AB上，AC＝3cm，BC＝2cm，点M、N分别是AC、BC的中点，则线段MN的长度为cm.
18. 如图，一工作流程线上有6位工人，他们的工作位置分别是A．B、C、D、E、F，现要在这六个位置之一设置一个工具箱，使工人取工具所花费的总时间最少．那么这个工具箱应放置在最合适．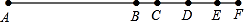
三、解答题
-
19. 在同一个学校上学的小明、小伟、小红三位同学住在A，B，C三个住宅区，如图所示（A，B，C在同一条直线上），且AB=60米，BC=100米，他们打算合租一辆接送车去上学，由于车位紧张，准备在周围只设一个停靠点，为使三位同学步行到停靠点的路程之和最小，你认为停靠点应该设在哪里？并说明理由．
20. OC是从∠AOB的顶点O引出的一条射线，若∠AOB=90°，∠AOB=2∠BOC，求∠AOC的度数．21. 地震后，许许多多志愿者到灾区投入了抗震救灾行列中．志愿者小方八点多准备前去为灾民服务，临出门他一看钟，时针与分针正好是重合的，下午两点多他拖着疲惫的身体回到家中，一进门看见钟的时针与分针方向相反，正好成一条直线，问小方是几点钟去为灾民服务？几点钟回到家？共用了多少时间？22. 在线段AB上顺次取三点C、D、E．(1)、若C、D、E是AB的四个等分点，画出图形，并求图中所有线段条数；(2)、若AB=12，求（1）中所有线段的长度；(3)、当C、D、E是线段上顺次三点时，若AB=12．CE=2，求图中所有线段的长度和．23. 如图，点C在线段AB上，线段AC=8cm，BC=4cm，点M、N分别是AC、BC的中点，求：
(1)、线段MN的长度．(2)、根据（1）的计算过程和结果，设AC+BC=a，其它条件不变，你能猜测出MN的长度吗？请证明你的猜测．24. 如图，点C在AB上，点M、N分别是AC、BC的中点，
(1)、若AC=12cm，BC=10cm，求线段MN的长；(2)、若点C为线段AB上任意一点，满足AC+BC=acm，其它条件不变，你能猜想MN的长度吗？并说明理由；(3)、若点C在线段AB的延长线上，且满足AC﹣BC=bcm，点M、N分别为AC、BC的中点，你能猜想MN的长度吗？请画出图形，并说明理由．请用一句简洁的话描述你发现的结论．25. 如图，∠A+∠B=90°，点D在线段AB上，点E在线段AC上，作直线DE，DF平分∠BDE，DF与BC交于点F．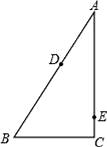
(1)、依题意补全图形；(2)、当∠B+∠BDF=90°时，∠A与∠EDF是否相等？说明理由．26. 如图1，∠AOB=α，∠COD=β，OM，ON分别是∠AOC，∠BOD的角平分线．
(1)、若∠AOB=50°，∠COD=30°，当∠COD绕着点O逆时针旋转至射线OB与OC重合时（如图2），则∠MON的大小为；(2)、在（1）的条件下，继续绕着点O逆时针旋转∠COD，当∠BOC=10°时（如图3），求∠MON的大小并说明理由；(3)、在∠COD绕点O逆时针旋转过程中，∠MON= ． （用含α，β的式子表示）．