湘教版七年级数学上册第三章一元一次方程单元检测b卷

试卷更新日期：2018-10-22 类型：单元试卷

进入出卷网下载

一、选择题

1. $\frac{3}{x}$ 的倒数与 $\frac{2 x - 9}{3}$ 互为相反数，那么 $x$ 的值是（）

A、 $\frac{3}{2}$ B、 $- \frac{3}{2}$ C、3 D、－3

查看试题解析
2. 闽北某村原有林地120公顷，旱地60公顷，为适应产业结构调整，需把一部分旱地改造为林地，改造后，旱地面积占林地面积的20%，设把x公顷旱地改造为林地，则可列方程为（）

A、60﹣x=20%（120+x） B、60+x=20%×120 C、180﹣x=20%（60+x） D、60﹣x=20%×120

查看试题解析
3. 方程2x－1＝3x＋2的解为（）

A、x＝1 B、x＝－1 C、x＝3 D、x＝－3

查看试题解析
4. 已知下列方程：①x﹣2= $\frac{1}{x}$ ；②0.2x=1；③ $\frac{x}{3} = x - 3$ ；④x﹣y=6；⑤x=0，其中一元一次方程有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
5. 互联网“微商”经营已成为大众创业新途径，某微信平台上一件商品标价为200元，按标价的五折销售，仍可获利20元，则这件商品的进价为（　　）

A、120元 B、100元 C、80元 D、60元

查看试题解析
6. 若关于x的方程2x+a﹣4=0的解是x=﹣2，则a的值等于（）

A、﹣8 B、0 C、2 D、8

查看试题解析
7. 若 $\frac{a}{3} + 1$ 与 $\frac{2 a - 7}{3}$ 互为相反数，则a=（）

A、 $\frac{4}{3}$ B、10 C、 $- \frac{4}{3}$ D、﹣10

查看试题解析
8. 医疗保险，住院治疗的病人享受分段报销，保险公司制定的报销细则如下表．某人住院治疗后得到保险公司报销金额是1100元，那么此人住院的医疗费是（）
住院医疗费（元）
报销率（%）
不超过500元的部分
0
超过500～1000元的部分
60
超过1000～3000元的部分
80
……

A、1000元 B、1250元 C、1500元 D、2000元

查看试题解析
9. 下列判断错误的是（）

A、若 $a = b$ ，则 $a c - 3 = b c - 3$ B、若 $a = b$ ，则 $\frac{a}{c^{2} + 1} = \frac{b}{c^{2} + 1}$ C、若 $x = 2$ ，则 $x^{2} = 2 x$ D、若 $a x = b x$ ，则 $a = b$

查看试题解析
10. 下面说法中 ①－a一定是负数；②0.5πab是二次单项式；③倒数等于它本身的数是±1；④若∣a∣=-a,则a＜0；⑤由-2（x-4）=2变形为x - 4 =-1，其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 一件衣服售价为200元，六折销售，仍可获利20%，则这件衣服的进价是元．

查看试题解析
12. 已知2a^3+mb⁵﹣pa⁴bⁿ⁺¹=7a⁴b⁵ ，则m+n+p= ．

查看试题解析
13. 已知关于 $x$ 的方程 $4 x + 2 m = 3 x + 1$ 与方程 $3 x + 2 m = 6 x + 1$ 的解相同，则方程的解为.

查看试题解析
14. 把一些图书分给某班学生阅读，如果每人3本，则剩余20本，如果每人4本，则还缺25本，那么这个班有学生．

查看试题解析
15. 若代数式x﹣3与5x﹣4的值相等，则x的值是．

查看试题解析
16. 在数学活动课上，老师说有人根据如下的证明过程，得到“1=2”的结论．
设a、b为正数，且a=b．
∵a=b，
∴ab=b² ． ①
∴ab﹣a²=b²﹣a² ． ②
∴a（b﹣a）=（b+a）（b﹣a）． ③
∴a=b+a．④
∴a=2a．⑤
∴1=2．⑥
大家经过认真讨论，发现上述证明过程中从某一步开始出现错误，这一步是（填入编号），造成错误的原因是．

查看试题解析
17. 规定一种运算“*”，a*b= $\frac{1}{3}$ a﹣ $\frac{1}{4}$ b，则方程x*2=1*x的解为．

查看试题解析

三、解答题

18. 解方程： $\frac{x}{0.7}$ ﹣ $\frac{1.7 - 2 x}{0.3}$ =1．

查看试题解析
19. 老师在黑板上出了一道解方程的题 $\frac{2 x - 1}{3} = 1 - \frac{x + 2}{4}$ ，小明马上举起了手，要求到黑板上去做，他是这样做的：
$4 (2 x - 1) = 1 - 3 (x + 2)$ ①
$8 x - 4 = 1 - 3 x - 6$ ②
$8 x + 3 x = 1 - 6 + 4$ ③
$11 x = - 1$ ④
$x = - \frac{1}{11}$ ⑤
老师说：小明解一元一次方程的一般步骤都掌握了，但解题时有一步做错了，请你指出他错在第几步（填编号）然后，细心地解下列方程：
$\frac{2 x + 1}{4} - \frac{x - 1}{3} = 2$ 相信你，一定能做对！

查看试题解析
20. 3个工程队合修一条公路，第一工程队修全路的 $\frac{1}{3}$ ，第二工程队修剩下的 $\frac{1}{3}$ ，第三工程队修了20千米把这条公路修完．这条公路共有多少千米？

查看试题解析
21. 甲、乙两商场以同样的价格出售同样的商品，并且又各自推出不同的优惠方案：在甲商场累计购物超过100元后，超出100元的部分按90%收费；在乙商场累计购物超过50元后，超出50元的部分按95%收费．设小红在同一商场累计购物x元，其中x>100.

(1)、根据题意，填写下表(单位：元)：

(2)、当x取何值时，小红在甲、乙两商场的实际花费相同？

(3)、当小红在同一商场累计购物超过100元时，在哪家商场的实际花费少？

查看试题解析
22. 定义新运算：对于任意有理数a，b，都有a⊗b=a（a﹣b）+1，等式右边是通常的加法、减法及乘法运算，比如：2⊗5=2×（2﹣5）+1=2×（﹣3）+1=﹣6+1=﹣5

(1)、求（﹣2）⊗3的值；

(2)、若4⊗x的值等于13，求x的值．

查看试题解析
23. 如图，已知数轴上有A．B、C三点，分别表示有理数﹣26、﹣10、10，动点P从点A出发，以每秒1个单位的速度向终点C移动，当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，问当点Q从A点出发几秒钟时，点P和点Q相距2个单位长度？直接写出此时点Q在数轴上表示的有理数．

查看试题解析
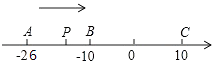24. 如图，将连续的偶数2，4，6，8，10，…排成一数阵，有一个能够在数阵中上下左右平移的T字架，它可以框出数阵中的五个数．试判断这五个数的和能否为426？若能，请求出这五个数；若不能，请说明理由．

查看试题解析
25. A．B、C为数轴上的三点，动点A．B同时从原点出发，动点A每秒运动x个单位，动点B每秒运动y个单位，且动点A运动到的位置对应的数记为a，动点B运动到的位置对应的数记为b，定点C对应的数为8．

(1)、若2秒后，a、b满足|a+8|+（b﹣2）²=0，则x= ， y= ，并请在数轴上标出A．B两点的位置．

(2)、若动点A．B在（1）运动后的位置上保持原来的速度，且同时向正方向运动z秒后使得|a|=|b|，使得z= ．

(3)、若动点A．B在（1）运动后的位置上都以每秒2个单位向正方向运动继续运动t秒，点A与点C之间的距离表示为AC，点B与点C之间的距离表示为BC，点A与点B之间的距离为AB，且AC+BC=1.5AB，则t= ．

查看试题解析

住院医疗费（元）	报销率（%）
不超过500元的部分	0
超过500～1000元的部分	60
超过1000～3000元的部分	80
……

湘教版七年级数学上册 第三章一元一次方程 单元检测b卷

一、选择题

二、填空题

三、解答题

湘教版七年级数学上册第三章一元一次方程单元检测b卷