2016-2017学年江西省萍乡市八年级上学期期末数学试卷
试卷更新日期:2017-03-10 类型:期末考试
一、选择题
-
1. 在平面直角坐标系中,已知点P(2,﹣3),则点P在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 估计 的值在( )A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间3. 下列语句中不是命题的是( )A、对顶角相等 B、过A,B两点作直线 C、两点之间线段最短 D、内错角相等4. 有19位同学参加歌咏比赛,所得的分数互不相同,取得前10位同学进入决赛.某同学知道自己的分数后,要判断自己能否进入决赛,他只需知道这19位同学的( )A、平均数 B、中位数 C、众数 D、方差5. 如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )
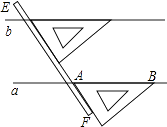 A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,内错角相等6. 若 +|y+2|=0,则(xy)2的值是|( )A、2 B、﹣2 C、4 D、﹣47. 小林家今年1﹣5月份的用电量情况如图所示.由图可知,相邻两个月中,用电量变化最大的是( )
A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,内错角相等6. 若 +|y+2|=0,则(xy)2的值是|( )A、2 B、﹣2 C、4 D、﹣47. 小林家今年1﹣5月份的用电量情况如图所示.由图可知,相邻两个月中,用电量变化最大的是( )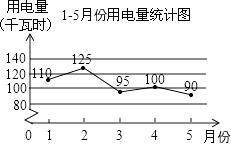 A、1月至2月 B、2月至3月 C、3月至4月 D、4月至5月8. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别是3,5,2,3,则最大正方形E的面积是( )
A、1月至2月 B、2月至3月 C、3月至4月 D、4月至5月8. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别是3,5,2,3,则最大正方形E的面积是( ) A、13 B、26 C、47 D、949. 楠溪江某景点门票价格:成人票每张70元,儿童票每张35元.小明买20张门票共花了1225元,设其中有x张成人票,y张儿童票,根据题意,下列方程组正确的是( )A、 B、 C、 D、10. 一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100千米/小时,特快车的速度为150千米/小时,甲、乙两地之间的距离为1000千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与快车行驶时间(小时)之间的函数图象是( )A、
A、13 B、26 C、47 D、949. 楠溪江某景点门票价格:成人票每张70元,儿童票每张35元.小明买20张门票共花了1225元,设其中有x张成人票,y张儿童票,根据题意,下列方程组正确的是( )A、 B、 C、 D、10. 一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100千米/小时,特快车的速度为150千米/小时,甲、乙两地之间的距离为1000千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与快车行驶时间(小时)之间的函数图象是( )A、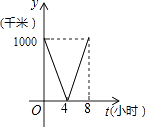 B、
B、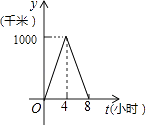 C、
C、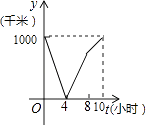 D、
D、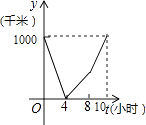
二、填空题
-
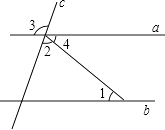
11. 计算: + = .12. 请你写出三组勾股数: .13. 八(1)班体育委员记录了某小姐七位同学定点投篮(每人投10个)的情况,投进篮筐的个数为6,10,5,3,4,8,4,则这组数据的众数、中位数、极差分别是 .14. 在一次函数y=(1﹣k)x﹣1中,函数y随x的增大而减小,请你写出一个符合条件的k的值:(写一个即可)15. 如图,直线a,b被直线c所截,若a∥b,∠1=40°,∠2=70°,则∠3=度.
 16. 如图,如果
16. 如图,如果 所在位置的坐标为(﹣1,﹣2),
所在位置的坐标为(﹣1,﹣2),  所在位置的坐标为(2,﹣2),那么,
所在位置的坐标为(2,﹣2),那么, 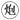 所在位置的坐标为 .
所在位置的坐标为 . 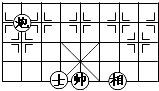 17. 如图,四边形ABCD中,点M、N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,∠A=100°,∠C=70°,则∠B= .
17. 如图,四边形ABCD中,点M、N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,∠A=100°,∠C=70°,则∠B= .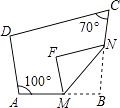 18. 如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(﹣2,0),(﹣1,0),BC⊥x轴,将△ABC以y轴为对称轴作轴对称变换,得到△A′B′C′(A和A′,B和B′,C和C′分别是对应顶点),直线y=x+b经过点A,C′,则点C′的坐标是 .
18. 如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(﹣2,0),(﹣1,0),BC⊥x轴,将△ABC以y轴为对称轴作轴对称变换,得到△A′B′C′(A和A′,B和B′,C和C′分别是对应顶点),直线y=x+b经过点A,C′,则点C′的坐标是 .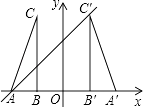
三、解答题
-
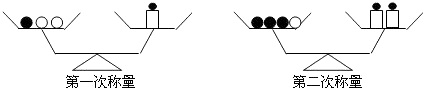
19. 计算下面各题(1)、解方程组:(2)、化简: ﹣3× + .20. 有黑白两种小球各若干个,且同色小球质量均相等,在如图所示的两次称量的天平恰好平衡,如果每只砝码质量均为5克,每只黑球和白球的质量各是多少克?
 21. 温度与我们的生活息息相关,你仔细观察过温度计吗?如图是一个温度计实物示意图,左边的刻度是摄氏温度(℃),右边的刻度是华氏温度(℉),设摄氏温度为x(℃),华氏温度为y(℉),则y是x的一次函数.
21. 温度与我们的生活息息相关,你仔细观察过温度计吗?如图是一个温度计实物示意图,左边的刻度是摄氏温度(℃),右边的刻度是华氏温度(℉),设摄氏温度为x(℃),华氏温度为y(℉),则y是x的一次函数. (1)、仔细观察图中数据,试求出y与x之间的函数表达式;(2)、当摄氏温度为零下15℃时,求华氏温度为多少?22. 将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)、仔细观察图中数据,试求出y与x之间的函数表达式;(2)、当摄氏温度为零下15℃时,求华氏温度为多少?22. 将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.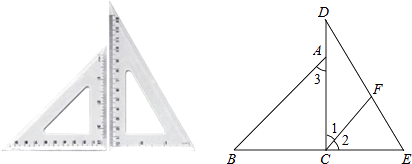 (1)、求证:CF∥AB;(2)、求∠DFC的度数.23. 某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.
(1)、求证:CF∥AB;(2)、求∠DFC的度数.23. 某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.
回答下列问题:
(1)、写出条形图中存在的错误,并说明理由;(2)、写出这20名学生每人植树量的众数、中位数;(3)、在求这20名学生每人植树量的平均数时,小宇是这样分析的:
①小宇的分析是从哪一步开始出现错误的?
②请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵.
24. 某校举办八年级学生数学素养大赛,比赛共设四个项目:七巧板拼图,趣题巧解,数学应用,魔方复原,每个项目得分都按一定百分比折算后记入总分,下表为甲,乙,丙三位同学得分情况(单位:分)七巧板拼图
趣题巧解
数学应用
魔方复原
甲
66
89
86
68
乙
66
60
80
68
丙
66
80
90
68
(1)、比赛后,甲猜测七巧板拼图,趣题巧解,数学应用,魔方复原这四个项目得分分别按10%,40%,20%,30%折算记入总分,根据猜测,求出甲的总分;(2)、本次大赛组委会最后决定,总分为80分以上(包含80分)的学生获一等奖,现获悉乙,丙的总分分别是70分,80分.甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分,问甲能否获得这次比赛的一等奖?25. 如图1,在平面直角坐标系中,A(0,1),B(4,1),C为x轴正半轴上一点,且AC平分∠OAB.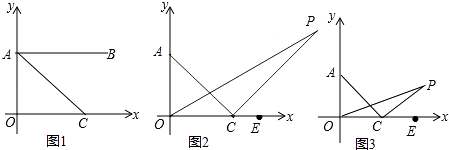 (1)、求证:∠OAC=∠OCA;(2)、如图2,若分别作∠AOC的三等分线及∠OCA的外角的三等分线交于点P,即满足∠POC= ∠AOC,∠PCE= ∠ACE,求∠P的大小;(3)、如图3,在(2)中,若射线OP、OC满足∠POC= ∠AOC,∠PCE= ∠ACE,猜想∠OPC的大小,并证明你的结论(用含n的式子表示)26. 如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上点E处.
(1)、求证:∠OAC=∠OCA;(2)、如图2,若分别作∠AOC的三等分线及∠OCA的外角的三等分线交于点P,即满足∠POC= ∠AOC,∠PCE= ∠ACE,求∠P的大小;(3)、如图3,在(2)中,若射线OP、OC满足∠POC= ∠AOC,∠PCE= ∠ACE,猜想∠OPC的大小,并证明你的结论(用含n的式子表示)26. 如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上点E处. (1)、求点E的坐标;(2)、求折痕CD所在直线的函数表达式;(3)、请你延长直线CD交x轴于点F.
(1)、求点E的坐标;(2)、求折痕CD所在直线的函数表达式;(3)、请你延长直线CD交x轴于点F.①求△COF的面积;
②在x轴上是否存在点P,使S△OCP= S△COF?若存在,求出点P的坐标;若不存在,请说明理由.