2016-2017学年江苏省泰州市兴化市顾庄学区三校八年级上学期期末数学试卷

试卷更新日期：2017-03-10 类型：期末考试

进入出卷网下载

一、选择题

1. 计算： $\sqrt{9}$ =（）

A、3 B、﹣3 C、±3 D、9

查看试题解析
2. 下面选项中既是中心对称图形又是轴对称图形的是（）

A、等边三角形 B、等腰梯形 C、菱形 D、五角星

查看试题解析
3. 下列事件中，必然事件是（　　）

A、抛掷1个均匀的骰子，出现6点向上 B、两直线被第三条直线所截，同位角相等 C、366人中至少有2人的生日相同 D、实数的绝对值是非负数

查看试题解析
4. 下列语句正确的是（）

A、平行四边形是轴对称图形 B、矩形的对角线相等 C、对角线互相垂直的四边形是菱形 D、对角线相等的四边形是矩形

查看试题解析
5. 将四根长度相等的细木条首尾相接，用钉子钉成四边形ABCD，转动这个四边形，使它形状改变，当∠B=90°时，如图1，测得AC=2，当∠B=60°时，如图2，AC=（）

A、 $\sqrt{2}$ B、2 C、 $\sqrt{6}$ D、2 $\sqrt{2}$

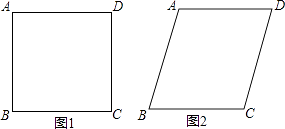查看试题解析
6. 已知直线y=kx+b不经过第三象限，则下列结论正确的是（）

A、k＞0，b＞0 B、k＜0，b＞0 C、k＜0，b＜0 D、k＜0，b≥0

查看试题解析

二、填空题

7. 在一副扑克牌中任意抽出一张牌，这张牌是大王的可能性比是红桃的可能性（填“大”或“小”）．

查看试题解析
8. 等腰三角形的顶角是70°，则其底角是．

查看试题解析
9. 某事件经过500000000次试验，出现的频率是0.3，它的概率估计值是．

查看试题解析
10. 一个学习兴趣小组有4名女生，6名男生，现要从这10名学生中选出一人担任组长，则女生当选组长的概率是．

查看试题解析
11. 若点A的坐标（a，b）满足条件（a+3）²+|b﹣2|=0，则点A在第象限．

查看试题解析
12. 已知函数y=（m﹣1）x+m²﹣1是正比例函数，则m=

查看试题解析
13. 已知函数y=2x+1和y=﹣x﹣2的图象交于点P，点P的坐标为（﹣1，﹣1），则方程组 ${\begin{matrix} 2 x - y + 1 = 0 \\ x + y + 2 = 0 \end{matrix}$ 的解为．

查看试题解析
14. ▱ABCD的对角线相交于点O，BC=7，BD=10，AC=6，则△AOD的周长是．

查看试题解析
15. 如图，点P是矩形ABCD的边AD上的一动点，矩形的两条边AB、BC的长分别是6和8，则点P到矩形的两条对角线AC和BD的距离之和是．

查看试题解析
16. 如图，已知A、B、C、D是平面直角坐标系中坐标轴上的点，且△AOB≌△COD，设直线AB的表达式为y₁=ax+b，直线CD的表达式为y₂=mx+n，则am= ．

查看试题解析

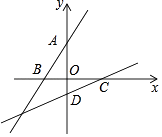
三、解答题

17. 计算下面各题

(1)、计算：（ $\sqrt{5}$ ）²﹣ $\sqrt[3]{- 8}$ ﹣|﹣3|+（﹣ $\frac{1}{5}$ ）⁰；

(2)、已知： $\frac{1}{3}$ （x+2）²﹣3=0，求x．

查看试题解析
18. 图1，图2都是8×8的正方形网格，每个小正方形的顶点成为格点，每个小正方形的边长均为1，在每个正方形网格中标注了6个格点，这6个格点简称为标注点

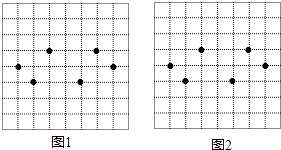(1)、请在图1，图2中，以4个标注点为顶点，各画一个平行四边形（两个平行四边形不全等）；

(2)、图1中所画的平行四边形的面积为．

查看试题解析
19. 等腰三角形的周长为80．

(1)、写出底边长y与腰长x的函数表达式，并写出自变量的取值范围；

(2)、当腰长为30时，底边长为多少？当底边长为8时，腰长为多少？

查看试题解析
20. 已知：如图，∠ABC=∠ADC=90°，E、F分别是AC、BD的中点．求证：EF⊥BD．

查看试题解析
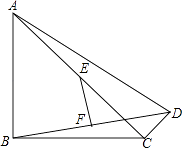21. △ABC的三边长分别是a、b、c，且a=m²﹣n² ， b=2mn，c=m²+n² ， △ABC是直角三角形吗？证明你的结论．

查看试题解析
22. 青少年“心理健康“问题越来越引起社会的关注，某中学为了了解学校600名学生的心理健康状况，举行了一次“心理健康“知识测试．并随机抽取了部分学生的成绩（得分取正整数，满分为100分）作为样本，绘制了下面未完成的频数分布表和频数分布直方图（如图）．请回答下列问题：
分组
频数
频率
50.5～60.5
4
0.08
60.5～70.5
14
0.28
70.5～80.5
16
     　
80.5～90.5

    　
90.5～100.5
10
0.20
合计

1.00

(1)、填写频数分布表中的空格，并补全频数分布直方图；

(2)、若成绩在70分以上（不含70分）为心理健康状况良好．若心理健康状况良好的人数占总人数的70%以上，就表示该校学生的心理健康状况正常，否则就需要加强心理辅导．请根据上述数据分析该校学生是否需要加强心理辅导，并说明理由．

查看试题解析
23. 如图，OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，求D、E两点的坐标．

查看试题解析
24. 如图，在Rt△ABC中，∠BAC=90°，D是BC的中点，M是AD 的中点，过点A作AN∥BC交BM的延长线于点N．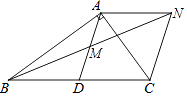

(1)、求证：△AMN≌△DMB；

(2)、求证：四边形ADCN是菱形．

查看试题解析
25. 已知y﹣3与x成正比例，且x=﹣2时，y=4．
①求出y与x之间的函数表达式；
②设点P（m，﹣1）在这个函数的图象上，求m的值．

查看试题解析
26. 代数式2x+3中，当x取a﹣3时，问2x+3是不是a的函数？若不是，请说明理由；若是，也请说明理由，并请以a的取值为横坐标，对应的2x+3值为纵坐标，画出其图象．

查看试题解析
27. 在平面直角坐标系xOy中，已知点A的坐标为（0，﹣1），点C（m，0）是x轴上的一个动点．

(1)、如图1，点B在第四象限，△AOB和△BCD都是等边三角形，点D在BC的上方，当点C在x轴上运动到如图所示的位置时，连接AD，请证明△ABD≌△OBC；

(2)、如图2，点B在x轴的正半轴上，△ABO和△ACD都是等腰直角三角形，点D在AC的上方，∠D=90°，当点C在x轴上运动（m＞1）时，设点D的坐标为（x，y），请探求y与x之间的函数表达式；

(3)、如图3，四边形ACEF是菱形，且∠ACE=90°，点E在AC的上方，当点C在x轴上运动（m＞1）时，设点E的坐标为（x，y），请探求y与x之间的函数表达式．

查看试题解析

分组	频数	频率
50.5～60.5	4	0.08
60.5～70.5	14	0.28
70.5～80.5	16
80.5～90.5
90.5～100.5	10	0.20
合计		1.00