2016-2017学年河北省唐山市路北区八年级上学期期末数学试卷

试卷更新日期：2017-03-10 类型：期末考试

进入出卷网下载

一、选择题

1. 式子 $\sqrt{x + 3}$ 有意义的条件是（）

A、x≥3 B、x＞3 C、x≥﹣3 D、x＞﹣3

查看试题解析
2. 下列平面图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列各式运算正确的是（）

A、 $\sqrt{4} = \pm 2$ B、4 $\sqrt{3} - \sqrt{3} = 4$ C、 $\sqrt{18} = 2 \sqrt{3}$ D、 $\sqrt{2} \cdot \sqrt{3} = \sqrt{6}$

查看试题解析
4. 一粒花粉的质量约为0.000037毫克，那么0.000037可用科学记数法表示为（）

A、3.7×10^﹣⁵ B、3.7×10^﹣⁶ C、37×10^﹣⁷ D、3.7×10^﹣⁸

查看试题解析
5. 若x²+6x+k是完全平方式，则k=（）

A、9 B、﹣9 C、±9 D、±3

查看试题解析
6. 把x³﹣2x²y+xy²分解因式，结果正确的是（）

A、x（x+y）（x﹣y） B、x（x²﹣2xy+y²） C、x（x+y）² D、x（x﹣y）²

查看试题解析
7. 化简 $\frac{a^{2} b - a b^{2}}{b - a}$ 结果正确的是（）

A、ab B、﹣ab C、a²﹣b² D、b²﹣a²

查看试题解析
8. 解分式方程 $\frac{2}{x - 1}$ + $\frac{x + 2}{1 - x}$ =3时，去分母后变形为（）

A、2+（x+2）=3（x﹣1） B、2﹣x+2=3（x﹣1） C、2﹣（x+2）=3（1﹣x） D、2﹣（x+2）=3（x﹣1）

查看试题解析
9. （3x+4y﹣6）²展开式的常数项是（）

A、﹣12 B、﹣6 C、9 D、36

查看试题解析
10. 如图，在△ABC中，点D在边BC上，若∠BAD=∠CAD，AB=6，AC=3，S_△_ABD=3，则S_△_ACD=（）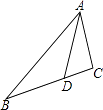

A、3 B、6 C、 $\frac{3}{2}$ D、 $\frac{9}{2}$

查看试题解析
11. 如图，在等腰三角形纸片ABC中，AB=AC，∠A=40°，折叠该纸片，使点A落在点B处，折痕为DE，则∠CBE的度数是（）

A、20° B、30° C、40° D、70°

查看试题解析
12. 如图，以∠AOB的顶点O为圆心，适当长为半径画弧，交OA于点C，交OB于点D，再分别以点C，D为圆心，大于 $\frac{1}{2}$ CD的长为半径画弧，两弧在∠AOB内部交于点E，过点E作射线OE，连接CD．则下列说法错误的是（）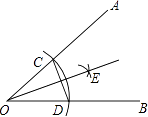

A、射线OE是∠AOB的平分线 B、△COD是等腰三角形 C、O，E两点关于CD所在直线对称 D、C，D两点关于OE所在直线对称

查看试题解析
13. 在平面直角坐标中，已知点P（a，5）在第二象限，则点P关于直线m（直线m上各点的横坐标都是2）对称的点的坐标是（　　）

A、（﹣a，5） B、（a，﹣5） C、（﹣a+2，5） D、（﹣a+4，5）

查看试题解析
14. 将边长分别为a+b和a﹣b的两个正方形摆放成如图所示的位置，则阴影部分的面积化简后的结果是（）

A、a﹣b B、a+b C、2ab D、4ab

查看试题解析

二、填空题

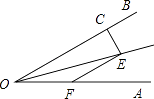
15. 25的算术平方根是．

查看试题解析
16. 若分式 $\frac{x^{2} - 1}{x + 1}$ 的值为0，则x= ．

查看试题解析
17. 如图，∠AOE=∠BOE=15°，EF∥OB，EC⊥OB，若EC=2，则EF= ．

查看试题解析
18. 一艘轮船在静水中的速度为a千米/时，若A、B两个港口之间的距离为50千米，水流的速度为b千米/时，轮船往返两个港口之间一次需小时．

查看试题解析

三、解答题

19. 计算：（2x+1）（x+3）．

查看试题解析
20. 计算：（ $\sqrt{48}$ + $\sqrt{27}$ ﹣ $\sqrt{12}$ ）÷ $\sqrt{6}$ ．

查看试题解析
21. 解方程： $\frac{2 x}{x + 3}$ +1= $\frac{7}{2 x + 6}$ ．

查看试题解析
22. 先化简，再求值： $\frac{x - 4}{x - 3}$ ÷（x+3﹣ $\frac{7}{x - 3}$ ），其中x=3．

查看试题解析
23. 已知：如图，AB∥CD，E是AB的中点，CE=DE．求证：

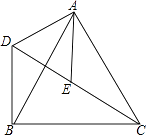
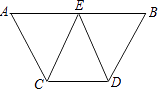(1)、∠AEC=∠BED；

(2)、AC=BD．

查看试题解析
24. 如图，△ACB和△ADE均为等边三角形，点C、E、D在同一直线上，连接BD．
求证：CE=BD．

查看试题解析
25. 随着城际铁路的正式开通，从甲市经丙市到乙市的高铁里程比普快里程缩短了90km，运行时间减少了8h，已知甲市到乙市的普快列车里程为1220km．高铁平均时速是普快平均时速的2.5倍．

(1)、求高铁列车的平均时速；

(2)、某日王先生要从甲市去距离大约780km的丙市参加14：00召开的会议，如果他买到当日9：20从甲市到丙市的高铁票，而且从丙市火车站到会议地点最多需要1小时．试问在高铁列车准点到达的情况下，它能否在开会之前20分钟赶到会议地点？

查看试题解析
26.
解答题

(1)、如图①，等腰直角△ABC中，∠ABC=90°，AB=BC，点A、B分别在坐标轴上，若点C的横坐标为2，直接写出点B的坐标；（提示：过C作CD⊥y轴于点D，利用全等三角形求出OB即可）

(2)、如图②，若点A的坐标为（﹣6，0），点B在y轴的正半轴上运动时，分别以OB、AB为边在第一、第二象限作等腰直角△OBF，等腰直角△ABE，连接EF交y轴于点P，当点B在y轴的正半轴上移动时，PB的长度是否发生改变？若不变，求出PB的值．若变化，求PB的取值范围．

查看试题解析