2016-2017学年河北省石家庄市高邑县八年级上学期期末数学试卷
试卷更新日期:2017-03-10 类型:期末考试
一、选择题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
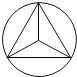 B、
B、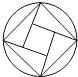 C、
C、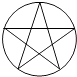 D、
D、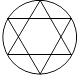 2. 若分式 的值为0,则( )A、x=﹣2 B、x=0 C、x=1 D、x=1或﹣23. 在0.51525354…、 、0.2、 、 、 、 中,无理数的个数是( )A、2 B、3 C、4 D、54. 下列说法中正确的是( )A、9的平方根为3 B、 化简后的结果是 C、 最简二次根式 D、﹣27没有立方根5. 下列运算中正确的是( )A、 B、 C、 D、6. 式子 有意义的x取值范围是( )A、x≠1 B、x≥﹣ C、x≥﹣ 且x≠1 D、x>﹣ 且x≠17. 化简 × 结果是( )A、 B、 C、 D、8. 已知等腰三角形的两条边长为1和 , 则这个三角形的周长为( )A、2+ B、1+2 C、2+2或1+2 D、1+9. 直角三角形的两边长分别是6,8,则第三边的长为( )A、10 B、2 C、10或2 D、无法确定10. 如图,一根木棍斜靠在与地面(OM)垂直的墙(ON)上,设木棍中点为P,若木棍A端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到点O的距离( )
2. 若分式 的值为0,则( )A、x=﹣2 B、x=0 C、x=1 D、x=1或﹣23. 在0.51525354…、 、0.2、 、 、 、 中,无理数的个数是( )A、2 B、3 C、4 D、54. 下列说法中正确的是( )A、9的平方根为3 B、 化简后的结果是 C、 最简二次根式 D、﹣27没有立方根5. 下列运算中正确的是( )A、 B、 C、 D、6. 式子 有意义的x取值范围是( )A、x≠1 B、x≥﹣ C、x≥﹣ 且x≠1 D、x>﹣ 且x≠17. 化简 × 结果是( )A、 B、 C、 D、8. 已知等腰三角形的两条边长为1和 , 则这个三角形的周长为( )A、2+ B、1+2 C、2+2或1+2 D、1+9. 直角三角形的两边长分别是6,8,则第三边的长为( )A、10 B、2 C、10或2 D、无法确定10. 如图,一根木棍斜靠在与地面(OM)垂直的墙(ON)上,设木棍中点为P,若木棍A端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到点O的距离( )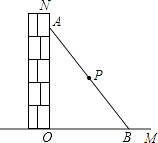 A、变小 B、不变 C、变大 D、无法判断11. 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A、变小 B、不变 C、变大 D、无法判断11. 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( ) A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD12. 如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE、下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )
A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD12. 如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE、下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( ) A、1个 B、2个 C、3个 D、4个13. 已知1≤a≤ ,化简 +|a﹣2|的结果是( )A、2a﹣3 B、2a+3 C、1 D、314. 某市需要铺设一条长660米的管道,为了尽量减少施工对城市交通造成的影响,实际施工时,每天铺设管道的长度比原计划增加10%,结果提前6天完成.求实际每天铺设管道的长度与实际施工天数.小宇同学根据题意列出方程 ﹣ =6.则方程中未知数x所表示的量是( )A、实际每天铺设管道的长度 B、实际施工的天数 C、原计划施工的天数 D、原计划每天铺设管道的长度15. 如图,已知AB=A1B,A1B1=A1B2 , A2B2=A2B3 , A3B3=A3B4 , …若∠A=70°,则∠An的度数为( )
A、1个 B、2个 C、3个 D、4个13. 已知1≤a≤ ,化简 +|a﹣2|的结果是( )A、2a﹣3 B、2a+3 C、1 D、314. 某市需要铺设一条长660米的管道,为了尽量减少施工对城市交通造成的影响,实际施工时,每天铺设管道的长度比原计划增加10%,结果提前6天完成.求实际每天铺设管道的长度与实际施工天数.小宇同学根据题意列出方程 ﹣ =6.则方程中未知数x所表示的量是( )A、实际每天铺设管道的长度 B、实际施工的天数 C、原计划施工的天数 D、原计划每天铺设管道的长度15. 如图,已知AB=A1B,A1B1=A1B2 , A2B2=A2B3 , A3B3=A3B4 , …若∠A=70°,则∠An的度数为( )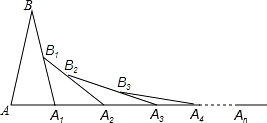 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
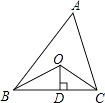
16. .(填“>”、“<”或“=”)17. 计算 的结果是 .18. 如图,已知△ABC的周长是24,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是 .
 19. 如图,在Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值为 .
19. 如图,在Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值为 .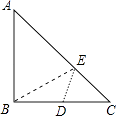
三、解答题
-
20. 先化简,再求值: ,其中x= ﹣1.21. 计算下面各题(1)、计算:(3﹣ )(3+ )+ (2﹣ )(2)、解方程: +1= .22. 如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
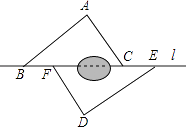 (1)、求证:△ABC≌△DEF;(2)、指出图中所有平行的线段,并说明理由.23. 在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
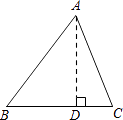
(1)、求证:△ABC≌△DEF;(2)、指出图中所有平行的线段,并说明理由.23. 在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.

 24. 甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的 ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.(1)、求乙骑自行车的速度;(2)、当甲到达学校时,乙同学离学校还有多远?25. 已知∠MAN=120°,AC平分∠MAN,点B、D分别在AN、AM上.
24. 甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的 ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.(1)、求乙骑自行车的速度;(2)、当甲到达学校时,乙同学离学校还有多远?25. 已知∠MAN=120°,AC平分∠MAN,点B、D分别在AN、AM上. (1)、如图1,若∠ABC=∠ADC=90°,请你探索线段AD、AB、AC之间的数量关系,并证明之;(2)、如图2,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
(1)、如图1,若∠ABC=∠ADC=90°,请你探索线段AD、AB、AC之间的数量关系,并证明之;(2)、如图2,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.