2018-2019学年初中数学九年级上学期期中模拟试卷（深圳专版）

试卷更新日期：2018-10-20 类型：期中考试

进入出卷网下载

一、选择题

1. 若方程（m﹣3）xⁿ+2x﹣3=0是关于x的一元二次方程，则（）

A、m=3，n≠2 B、m=3，n=2 C、m≠3，n=2 D、m≠3，n≠2

查看试题解析
2. 一元二次方程y²﹣y﹣ $\frac{3}{4}$ =0配方后可化为（）

A、（y+ $\frac{1}{2}$ ）²=1 B、（y﹣ $\frac{1}{2}$ ）²=1 C、（y+ $\frac{1}{2}$ ）²= $\frac{3}{4}$ D、（y﹣ $\frac{1}{2}$ ）²= $\frac{3}{4}$

查看试题解析
3. 在一个不透明的盒子里有n个除颜色外其他均相同的小球，其中有8个黄球，采用有放回的方式摸球，结果发现摸到黄球的频率稳定在40%，那么可以推算出n大约是（）

A、8 B、20 C、32 D、40

查看试题解析
4. 若α、β为方程 $2 x^{2} - 5 x - 1 = 0$ 的两个实数根，则 $2 α^{2} + 3 α β + 5 β$ 的值为（）。

A、 B、12 C、14 D、15

查看试题解析
5. 下列命题正确的是（）

A、对角线相等的四边形是平行四边形 B、对角线相等的四边形是矩形 C、对角线互相垂直的平行四边形是菱形 D、对角线互相垂直且相等的四边形是正方形

查看试题解析
6. 如图，某小区计划在一块长为32m，宽为20m的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为570m² ．若设道路的宽为 $x m$ ，则下面所列方程正确的是（）

A、 $(32 - x) (20 - x) = 32 \times 20 - 570$ B、 $32 x + 2 \times 20 x = 32 \times 20 - 570$ C、 $32 x + 2 \times 20 x - 2 x^{2} = 570$ D、 $(32 - 2 x) (20 - x) = 570$

查看试题解析
7. 关于x的方程kx²+3x﹣1=0有实数根，则k的取值范围是（）

A、k≤ $\frac{9}{4}$ B、k≥﹣ $\frac{9}{4}$ 且k≠0 C、k≥﹣ $\frac{9}{4}$ D、k＞﹣ $\frac{9}{4}$ 且k≠0

查看试题解析
8. 在Rt△ABC中，斜边AB=5，而直角边BC，AC之长是一元二次方程x²-（2m-1）x+4（m-1）=0的两根，则m的值是（）

A、4 B、-1 C、4或-1 D、-4或1

查看试题解析
9. 如图是由8个全等的矩形组成的大正方形，线段AB的端点都在小矩形的顶点上，如果点P是某个小矩形的顶点，连接PA、PB，那么使△ABP为等腰直角三角形的点P的个数是（）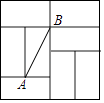

A、2个 B、3个 C、4个 D、5个

查看试题解析
10. 如图，在菱形ABCD中，点E，F，G，H分别是边AB，BC，CD和DA的中点，连接EF，FG，GH和HE，若EH＝2EF，则下列结论正确的是（）

A、AB＝ $\sqrt{2}$ EF B、AB＝2EF C、AB＝ $\sqrt{3}$ EF D、AB＝ $\sqrt{5}$ EF

查看试题解析
11. 如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高．得到下面四个结论：①OA=OD；②AD⊥EF；③当∠A=90°时，四边形AEDF是正方形；④ $A E^{2} + D F^{2} = A F^{2} + D E^{2}$ ．上述结论中正确的是（）

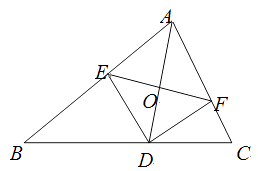A、②③ B、②④ C、①②③ D、②③④

查看试题解析

二、填空题

12. 要使平行四边形ABCD是矩形，还需添加的条件是(写出一种即可).

查看试题解析
13. 等腰三角形的底和腰是方程x²﹣6x+8=0的两根，则这个三角形的周长为．

查看试题解析
14.
如图，在Rt△ABC中，∠BAC=90°，AB=6，AC=8，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值是．

查看试题解析
15. 对于任意实数a、b，定义：a◆b=a²+ab+b² ．若方程（x◆2）﹣5=0的两根记为m、n，则m²+n²= ．

查看试题解析

三、解答题

16. 按指定的方法解下列方程：

(1)、2x²-5x-4=0（配方法）；

(2)、3（x-2）+x²-2x=0（因式分解法）；

(3)、（a²-b²）x²-4abx=a²-b²（a²≠b²）（公式法）．

查看试题解析
17. 已知关于x的方程 $x^{2} - 2 m x + m^{2} + m - 2 = 0$ 有两个不相等的实数根．

(1)、求m的取值范围；

(2)、当m为正整数时，求方程的根．

查看试题解析
18. 某单位组织职工观光旅游，旅行社的收费标准是：如果人数不超过25人，人均旅游费用为100元；如果超过25人，每增加1人，人均旅游费用降低2元，但人均旅游费用不得低于70元．该单位按旅行社的收费标准组团，结束后，共支付给旅行社2700元．求该单位这次共有多少人参加旅游？

查看试题解析
19. 阅读下面的材料，解答问题：为解方（x²﹣1）²﹣5（x²﹣1）+6=0．我们可以将（x²﹣1）看作一个整体，然后x²﹣1=y，那么原方程可化为y²﹣5y+6=0，解得y₁=2，y₂=3．
当y=2时，x²﹣1=2，x²=3，x=± $\sqrt{3}$ ；
当y=3时，x²﹣1=3，x²=4，x=±2．
当原方程的解为x₁= $\sqrt{3}$ ， x₂=﹣ $\sqrt{3}$ ， x₃=2，x₄=﹣2．
上述解题方法叫做“换元法”；请利用“换元法”解方程．（x²+x）²﹣4（x²+x）﹣12=0．

查看试题解析
20. 如图，在▱ABCD中，AE⊥BC，AF⊥CD，垂足分别为E，F，且BE=DF．

(1)、求证：▱ABCD是菱形；

(2)、若AB=5，AC=6，求▱ABCD的面积．

查看试题解析
21. 已知菱形的一个角与三角形的一个角重合，然后它的对角顶点在这个重合角的对边上，这个菱形称为这个三角形的亲密菱形，如图，在△CFE中，CF=6，CE=12，∠FCE=45°，以点C为圆心，以任意长为半径作AD，再分别以点A和点D为圆心，大于 $\frac{1}{2}$ AD长为半径做弧，交 $E F$ 于点B，AB∥CD.

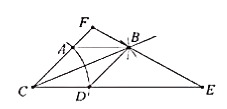(1)、求证：四边形ACDB为△CFE的亲密菱形；

(2)、求四边形ACDB的面积.

查看试题解析
22. 如图，3×3的方格分为上中下三层，第一层有一枚黑色方块甲，可在方格A、B、C中移动，第二层有两枚固定不动的黑色方块，第三层有一枚黑色方块乙，可在方格D、E、F中移动，甲、乙移入方格后，四枚黑色方块构成各种拼图．

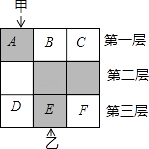(1)、若乙固定在E处，移动甲后黑色方块构成的拼图是轴对称图形的概率是．

(2)、若甲、乙均可在本层移动．
①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率．
②黑色方块所构拼图是中心对称图形的概率是．

查看试题解析