2017年四川省自贡市高考数学一诊试卷（理科）

试卷更新日期：2017-03-10 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知集合 $A = {x | \frac{x + 3}{x - 3} \leq 0}$ ，B={x|x﹣1≥0}，则A∩B为（）

A、[1，3] B、[1，3） C、[﹣3，∞） D、（﹣3，3]

查看试题解析
2. 已知复数 $z = \frac{1}{1 + i} + i$ ，则z在复平面内对应的点在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 已知函数f（x）的定义域为R，M为常数．若p：对∀x∈R，都有f（x）≥M；q：M是函数f（x）的最小
值，则p是q的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 如果a₁ ， a₂ ， …，a₈为各项都大于零的等差数列，公差d≠0，则（）

A、a₁a₈＞a₄a₅ B、a₁a₈＜a₄a₅ C、a₁+a₈＞a₄+a₅ D、a₁a₈=a₄a₅

查看试题解析
5. 已知 $\cos (α + \frac{2}{3} π) = \frac{4}{5} ， - \frac{π}{2} < α < 0$ ，则 $\sin (α + \frac{π}{3}) + \sin α$ 等于（）

A、 $- \frac{4 \sqrt{3}}{5}$ B、 $- \frac{3 \sqrt{3}}{5}$ C、 $\frac{3 \sqrt{3}}{5}$ D、 $\frac{4 \sqrt{3}}{5}$

查看试题解析
6. 已知集合A={5}，B={1，2}，C={1，3，4}，从这三个集合中各取一个元素构成空间直角坐标系上的坐标，则确定的不同点的个数为（）

A、6 B、32 C、33 D、34

查看试题解析
7. 设 $f (x) = x^{3} + \log_{2} (x + \sqrt{x^{2} + 1})$ ，则对任意实数a、b，若a+b≥0则（）

A、f（a）+f（b）≤0 B、f（a）+f（b）≥0 C、f（a）﹣f（b）≤0 D、f（a）﹣f（b）≥0

查看试题解析
8. 某企业节能降耗技术改造后，在生产某产品过程中几录的产量x（吨）与相应的生产能耗y（吨）的几
组对应数据如表所示：
x
3
4
5
6
y
2.5
3
4
a
若根据表中数据得出y关于x的线性回归方程为 $\hat{y}$ =0.7x+0.35，则表中a的值为（）

A、3 B、3.15 C、3.5 D、4.5

查看试题解析
9. 将函数 $y = 2 \sin (2 x + \frac{π}{6})$ 的图象向右平移 $\frac{1}{4}$ 个周期后，所得图象对应的函数为f（x），则函数f（x）的单
调递增区间（）

A、 $[k π - \frac{π}{12} ， k π + \frac{5 π}{12}] (k \in z)$ B、 $[k π + \frac{5 π}{12} ， k π + \frac{11 π}{12}] (k \in z)$ C、 $[k π - \frac{5 π}{24} ， k π + \frac{7 π}{24}] (k \in z)$ D、 $[k π + \frac{7 π}{24} ， k π + \frac{19 π}{24}] (k \in z)$

查看试题解析
10. 已知a∈{0，1，2}，b∈{﹣1，1，3，5}，则函数f（x）=ax²﹣2bx在区间（1，+∞）上为增函数的概率是（）

A、 $\frac{5}{12}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
11. 若正整数N除以正整数m后的余数为n，则记为N=n（bmodm），例如10=2（bmod4）．如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》．执行该程序框图，则输出的n等于（）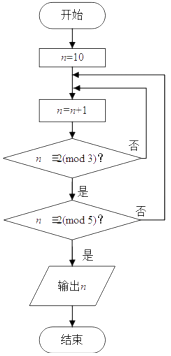

A、20 B、21 C、22 D、23

查看试题解析
12. 设函数f（x）=e^x（3x﹣1）﹣ax+a，其中a＜1，若有且只有一个整数x₀使得f（x₀）≤0，则a的取值范
围是（）

A、 $(\frac{2}{e} ， \frac{3}{4})$ B、 $[\frac{2}{e} ， \frac{3}{4})$ C、 $(\frac{2}{e} ， 1)$ D、 $[\frac{2}{e} ， 1)$

查看试题解析

二、填空题

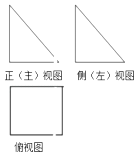
13. 在边长为1的正三角形ABC中，设 $\vec{B C} = 2 \vec{B D}$ ， $\vec{C A} = 3 \vec{C E}$ ，则 $\vec{A D} \cdot \vec{B E}$ = ．

查看试题解析
14. 设x，y满足约束条件 ${\begin{matrix} x + y - 7 \leq 0 \\ x - 3 y + 1 \leq 0 \\ 3 x - y - 5 \geq 0 \end{matrix}$ ，则z=2x﹣y的最大值为．

查看试题解析
15. 已知一个多面体的三视图如图示：其中正视图与侧视图都是边长为1的等腰直角三角形，俯视图是边长为1的正方形，若该多面体的顶点都在同一个球面上，则该球的表面积为．

查看试题解析
16. 设f'（x）是函数f（x）的导数，f''（x）是函数f'（x）的导数，若方程f''（x）=0有实数解x₀ ，则称点（x₀ ， f（x₀））为函数f（x）的拐点．某同学经过探究发现：任何一个三次函数f（x）=ax³+bx²+cx+d（a≠0）都有拐点，任何一个三次函数都有对称中心，且拐点就是对称中心，
设函数g（x）=x³﹣3x²+4x+2，利用上述探究结果
计算： $g (\frac{1}{10}) + g (\frac{2}{10}) + g (\frac{3}{10}) + \dots + g (\frac{9}{10})$ =

查看试题解析

三、解答题

17. 在△ABC中，A，B，C的对边分别为a、b、c， $C = \frac{π}{3} ， b = 8$ ，△ABC的面积为 $10 \sqrt{3}$ ．
（Ⅰ）求c的值；
（Ⅱ）求cos（B﹣C）的值．

查看试题解析
18. 已知数列{a_n}是公差为2的等差数列，数列{b_n}满足 $b_{1} = 1 ， b_{2} = \frac{1}{2}$ ，若n∈N^*时，a_nb_n₊₁﹣b_n₊₁=nb_n ．
（Ⅰ）求{b_n}的通项公式；
（Ⅱ）设c_n=a_nb_n ，求{c_n}的前n项和S_n ．

查看试题解析
19. 甲、乙两位射击运动员，在某天训练中已各射击10次，每次命中的环数如下：
甲 7 8 7 9 5 4 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
（Ⅰ）通过计算估计，甲、乙二人的射击成绩谁更稳；
（Ⅱ）若规定命中8环及以上环数为优秀，以频率作为概率，请依据上述数据估计，求甲在第11至
第13次射击中获得获得优秀的次数ξ的分布列和期望．

查看试题解析
20. 如图，三棱柱ABC﹣A₁B₁C₁中，侧面AA₁C₁C⊥底面ABC，AA₁=A₁C=AC=2，AB=BC且AB⊥BC，
（Ⅰ）求证：AC⊥A₁B；
（Ⅱ）求二面角A﹣A₁C﹣B的余弦值．

查看试题解析
21. 已知函数f（x）=f'（1）e^x^﹣¹﹣f（0）x+ $\frac{1}{2} x^{2} (f^{'} (x)) 是 f (x)$ 的导数，e为自然对数的底数）g（x）= $\frac{1}{2} x^{2}$ +ax+b（a∈R，b∈R）
（Ⅰ）求f（x）的解析式及极值；
（Ⅱ）若f（x）≥g（x），求 $\frac{b (a + 1)}{2}$ 的最大值．

查看试题解析
22. 在平面直角坐标系中，直线l的参数方程为 ${\begin{matrix} x = - 1 + \frac{\sqrt{2}}{2} t \\ y = - 5 + \frac{\sqrt{2}}{2} t \end{matrix}$ （其中t为参数），现以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C的极坐标方程为ρ=4cosθ．
（Ⅰ）写出直线l和曲线C的普通方程；
（Ⅱ）已知点P为曲线C上的动点，求P到直线l的距离的最小值．

查看试题解析
23. 已知a是常数，对任意实数x，不等式|x+1|﹣|2﹣x|≤a≤|x+1|+|2﹣x|都成立．
（Ⅰ）求a的值；
（Ⅱ）设m＞n＞0，求证：2m+ $\frac{1}{m^{2} - 2 m n + n^{2}}$ ≥2n+a．

查看试题解析

x	3	4	5	6
y	2.5	3	4	a