2017年四川省省级联考高考数学模拟试卷（理科）

试卷更新日期：2017-03-10 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知i是虚数单位，复数（2+i）²的共轭复数为（）

A、3﹣4i B、3+4i C、5﹣4i D、5+4i

查看试题解析
2. 设向量 $\vec{m}$ =（2x﹣1，3），向量 $\vec{n}$ =（1，﹣1），若 $\vec{m}$ ⊥ $\vec{n}$ ，则实数x的值为（）

A、﹣1 B、1 C、2 D、3

查看试题解析
3. 设集合A={﹣1，1}，集合B={x|ax=1，a∈R}，则使得B⊆A的a的所有取值构成的集合是（）

A、{0，1} B、{0，﹣1} C、{1，﹣1} D、{﹣1，0，1}

查看试题解析
4. 执行如图所示的程序框图，输出S的值为（）

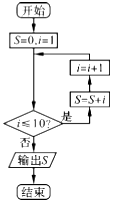A、45 B、55 C、66 D、110

查看试题解析
5. 小孔家有爷爷、奶奶、姥爷、姥姥、爸爸、妈妈，包括他共7人，一天爸爸从果园里摘了7个大小不同的梨，给家里每人一个，小孔拿了最小的一个，爷爷、奶奶、姥爷、姥姥4位老人之一拿最大的一个，则梨子的不同分法共有（）

A、96种 B、120种 C、480种 D、720种

查看试题解析
6. 函数 $f (x) = A \sin (ω x + ϕ) (A > 0 ， ω > 0 ， | ϕ | < \frac{π}{2})$ 的部分图象如图所示，则函数f（x）的解析式为（）

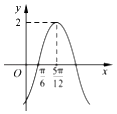A、 $f (x) = 2 \sin (x - \frac{π}{6})$ B、 $f (x) = 2 \sin (2 x - \frac{π}{3})$ C、 $f (x) = 2 \sin (x + \frac{π}{12})$ D、 $f (x) = 2 \sin (2 x - \frac{π}{6})$

查看试题解析
7. 设直角坐标平面内与两个定点A（﹣2，0），B（2，0）的距离之差的绝对值等于2的点的轨迹是E，C是轨迹E上一点，直线BC垂直于x轴，则 $\vec{A C} \cdot \vec{B C}$ =（）

A、﹣9 B、﹣3 C、3 D、9

查看试题解析
8. 利用计算机产生120个随机正整数，其最高位数字（如：34的最高位数字为3，567的最高位数字为5）的频数分布图如图所示，若从这120个正整数中任意取出一个，设其最高位数字为d（d=1，2，…，9）的概率为P，下列选项中，最能反映P与d的关系的是（）

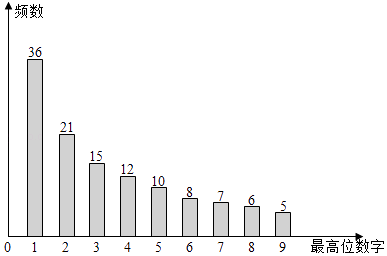A、P=lg（1+ $\frac{1}{d}$ ） B、P= $\frac{1}{d + 2}$ C、P= $\frac{{(d - 5)}^{2}}{120}$ D、P= $\frac{3}{5}$ × $\frac{1}{2^{d}}$

查看试题解析
9. 如图，A₁ ， A₂为椭圆 $\frac{x^{2}}{9} + \frac{y^{2}}{5}$ =1的长轴的左、右端点，O为坐标原点，S，Q，T为椭圆上不同于A₁ ， A₂的三点，直线QA₁ ， QA₂ ， OS，OT围成一个平行四边形OPQR，则|OS|²+|OT|²=（）

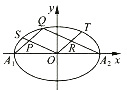A、5 B、3+ $\sqrt{5}$ C、9 D、14

查看试题解析
10. 设a，b是不相等的两个正数，且blna﹣alnb=a﹣b，给出下列结论：①a+b﹣ab＞1；②a+b＞2；③ $\frac{1}{a}$ + $\frac{1}{b}$ ＞2．其中所有正确结论的序号是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析

二、填空题

11. 在（2 $\sqrt{x}$ ﹣ $\frac{1}{\sqrt{x}}$ ）⁶的展开式中，含x³项的系数是（用数字填写答案）

查看试题解析
12. 一个几何体的三视图如图所示，则几何体的体积为．

查看试题解析
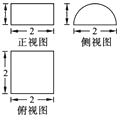13. 已知tanα=3，则sinαsin（ $\frac{3 π}{2}$ ﹣α）的值是．

查看试题解析
14. 已知圆的方程为x²+y²﹣6x=0，过点（1，2）的该圆的三条弦的长a₁ ， a₂ ， a₃构成等差数列，则数列a₁ ， a₂ ， a₃的公差的最大值是

查看试题解析
15. 已知 $\vec{O A}$ =（1，0）， $\vec{O B}$ =（1，1），（x，y）= $λ \vec{O A} + μ \vec{O B}$ ，若0≤λ≤1≤μ≤2时，z= $\frac{x}{m} + \frac{y}{n}$ （m＞0，n＞0）的最大值为2，则m+n的最小值为

查看试题解析

三、解答题

16. 在△ABC中，角A，B，C所对的边分别为a，b，c，且满足acosB=bcosA．

(1)、判断△ABC的形状；

(2)、求sin（2A+ $\frac{π}{6}$ ）﹣2cos²B的取值范围．

查看试题解析
17. 设数列{a_n}各项为正数，且a₂=4a₁ ， a_n₊₁= $a_{n}^{2}$ +2a_n（n∈N^*）
（I）证明：数列{log₃（1+a_n）}为等比数列；
（Ⅱ）令b_n=log₃（1+a_2n_﹣₁），数列{b_n}的前n项和为T_n ，求使T_n＞345成立时n的最小值．

查看试题解析
18. 某商场进行有奖促销活动，顾客购物每满500元，可选择返回50元现金或参加一次抽奖，抽奖规则如下：从1个装有6个白球、4个红球的箱子中任摸一球，摸到红球就可获得100元现金奖励，假设顾客抽奖的结果相互独立．
（Ⅰ）若顾客选择参加一次抽奖，求他获得100元现金奖励的概率；
（Ⅱ）某顾客已购物1500元，作为商场经理，是希望顾客直接选择返回150元现金，还是选择参加3次抽奖？说明理由；
（Ⅲ）若顾客参加10次抽奖，则最有可能获得多少现金奖励？

查看试题解析
19. 如图，在正方形ABCD中，点E，F分别是AB，BC的中点．将△AED，△DCF分别沿DE，DF折起，使A，C两点重合于P．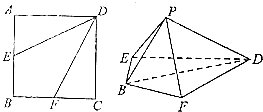

(1)、求证：平面PBD⊥平面BFDE；

(2)、求二面角P﹣DE﹣F的余弦值．

查看试题解析
20.
已知直线l的方程为y=x+2，点P是抛物线y²=4x上到直线l距离最小的点，点A是抛物线上异于点P的点，直线AP与直线l交于点Q，过点Q与x轴平行的直线与抛物线y²=4x交于点B．

（Ⅰ）求点P的坐标；
（Ⅱ）证明直线AB恒过定点，并求这个定点的坐标．

查看试题解析
21. 设a，b∈R，函数 $f (x) = \frac{1}{3} x^{3} + a x^{2} + b x + 1$ ，g（x）=e^x（e为自然对数的底数），且函数f（x）的图象与函数g（x）的图象在x=0处有公共的切线．
（Ⅰ）求b的值；
（Ⅱ）讨论函数f（x）的单调性；
（Ⅲ）若g（x）＞f（x）在区间（﹣∞，0）内恒成立，求a的取值范围．

查看试题解析