湘教版八年级数学上册第五章 二次根式 单元检测卷
试卷更新日期:2018-10-19 类型:单元试卷
一、选择题
-
1. 计算|2﹣ |+|4﹣ |的值是( )A、﹣2 B、2 C、2 ﹣6 D、6﹣22. 化简二次根式 的结果是( )A、﹣a B、 C、|a| D、a3. 下列各组二次根式中,x的取值范围相同的是( )A、 与 B、( )2与 C、 与 D、 与4. 已知 ,则
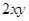 的值为( ) A、
的值为( ) A、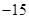 B、15
C、
B、15
C、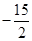 D、
5. 已知 是整数,则满足条件的最小正整数n为( )A、2 B、3 C、4 D、56. 在下列各式的化简中,化简正确的有( )
D、
5. 已知 是整数,则满足条件的最小正整数n为( )A、2 B、3 C、4 D、56. 在下列各式的化简中,化简正确的有( )①=a , ②5x﹣=4x , ③6a= , ④+=10
A、1个 B、2个 C、3个 D、4个7. 下列各实数中最大的一个是( )A、5× B、 C、 D、 +8. ( ﹣2)2008( +2)2007的值等于( )A、2 B、﹣2 C、 D、9. 与 不是同类二次根式的是( )A、 B、 C、 D、10. 已知 , ,且(7m2﹣14m+a)(3n2﹣6n﹣7)=8,则a的值等于( )A、﹣5 B、5 C、﹣9 D、911. 已知a是1997的算术平方根的整数部分,b是1991的算术平方根的小数部分,则化简 的结果为( )A、 B、 C、 D、12. 计算: =( )A、 B、 C、 D、二、填空题
-
13. 观察分析下列数据,寻找规律:0,- , ,- ,2 ,-5, ,…则第100个数据应是 .14. 对于X,Y定义一种新运算“*”:X*Y=aX+bY,其中a,b为常数,等式右边是通常的加法和乘法的运算.若 成立,那么2*3= .15. 如果(x﹣ )(y﹣ )=2008,求3x2﹣2y2+3x﹣3y﹣2007= .16. 已知:x= ,y= ,那么x2+y2的值为 .17. 已知x1= + ,x2= ﹣ ,则x12+x22= .
18. 设 的整数部分是a,小数部分是b,则 的值是 .三、解答题
-
19. 计算:
(1)、(2)、 .20. 小东在学习了 后, 认为 也成立, 因此他认为一个化简过程: = 是正确的. 你认为他的化简对吗?如果不对请说明理由并改正.21. 观察下列格式, - , , , …(1)、化简以上各式,并计算出结果;(2)、以上格式的结果存在一定的规律,请按规律写出第5个式子及结果(3)、用含n(n≥1的整数)的式子写出第n个式子及结果,并给出证明的过程.22. 对于“化简并求值: + , 其中a= ”,甲、乙两人的解答不同.甲的解答是: + = + = + ﹣a= ﹣a= ;
乙的解答是: + = + = +a﹣ =a= .
(1)、的解答是错误的;(2)、错误的解答在于未能正确运用二次根式的性质: .(3)、化简并求值:|1﹣a|+ ,其中a=2.23.(1)、要使 在实数范围内有意义,求x的取值范围;(2)、实数x,y满足条件:y= + + ,求(x+y)100的值.
