沪科版八年级数学上册 12.3 一次函数与二元一次方程同步练习

试卷更新日期：2018-10-19 类型：同步测试

进入出卷网下载

一、选择题

1. 已知直线经过点A（-1，2）且与x轴交于点B，点B的坐标是（）

A、（-3，0） B、（0，3） C、（3，0） D、（0，-3）

查看试题解析
2. 若方程组 ${\begin{matrix} - m x + y = n \\ e x + y = f \end{matrix}$ 的解为 ${\begin{matrix} x = 4 \\ y = 6 \end{matrix}$ ，则直线y=mx+n与y=﹣ex+f的交点坐标为（）

A、（﹣4，6） B、（4，6） C、（4，﹣6） D、（﹣4，﹣6）

查看试题解析
3. 函数y=4x﹣2与y=﹣4x﹣2的交点坐标为（）

A、（﹣2，0） B、（0，﹣2） C、（0，2） D、（2，0）

查看试题解析
4. 若一次函数y₁=k₁x+b₁与一次函数y₂=k₂x+b₂的图象没有交点，则方程组 ${\begin{matrix} k_{1} x - y = - b_{1} \\ k_{2} x - y = - b_{2} \end{matrix}$ 的解的情况是（）

A、有无数组解 B、有两组解 C、只有一组解 D、没有解

查看试题解析
5. 直线y=kx+b过点（2，2）且与直线y=-3x相交于点（1，a），则两直线与x轴所围成的面积为（）

A、2 B、2.4 C、3 D、4.8

查看试题解析
6. 已知直线y＝－x＋4与y＝x＋2如图所示，则方程组 ${\begin{matrix} y = - x + 4 \\ y = x + 2 \end{matrix}$ 的解为（）

A、 ${\begin{matrix} x = 3 \\ y = 1 \end{matrix}$ B、 ${\begin{matrix} x = 1 \\ y = 3 \end{matrix}$ C、 ${\begin{matrix} x = 0 \\ y = 4 \end{matrix}$ D、 ${\begin{matrix} x = 4 \\ y = 0 \end{matrix}$

查看试题解析
7. 如图，在平面直角坐标系中，直线l₁：y=x+3与直线l₂：y=mx+n交于点A（﹣1，b），则关于x、y的方程组 ${\begin{matrix} y = x + 3 \\ y = m x + n \end{matrix}$ 的解为（）

A、 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ B、 ${\begin{matrix} x = 2 \\ y = - 1 \end{matrix}$ C、 ${\begin{matrix} x = - 1 \\ y = 2 \end{matrix}$ D、 ${\begin{matrix} x = - 1 \\ y = - 2 \end{matrix}$

查看试题解析
8. 图中两直线l₁ ， l₂的交点坐标可以看作方程组（）的解．

A、 ${\begin{matrix} x - y = 1 \\ 2 x - y = - 1 \end{matrix}$ B、 ${\begin{matrix} x - y = - 1 \\ 2 x - y = 1 \end{matrix}$ C、 ${\begin{matrix} x - y = 3 \\ 2 x - y = 1 \end{matrix}$ D、 ${\begin{matrix} x - y = 3 \\ 2 x - y = - 1 \end{matrix}$

查看试题解析

二、填空题

9. 如图，已知函数y=ax+b和y=cx+d的图象交于点M，则根据图象可知，关于x，y的二元一次方程组 ${\begin{matrix} y = a x + b \\ y = c x + d \end{matrix}$ 的解为．

查看试题解析
10. 如图，函数y=kx+b的图象与x轴，y轴分别交于A（﹣2，0），B（0，1）两点，那么此函数的图象与函数y=x﹣1的图象交点C的坐标是．

查看试题解析
11. 已知直线y=2x+1和y=3x+b的交点在第二象限，则b的取值范围是．

查看试题解析
12. 若点P(1，1)在直线 $l_{1}$ ：y=kx+2上，点 Q(m， 2m -1)在直线 $l_{2}$ 上，则直线 $l_{1}$ 和 $l_{2}$ 的交点坐标是．

查看试题解析
13. 方程组 ${\begin{matrix} 2 x + y = 2 \\ 2 x + y = 5 \end{matrix}$ 的解为，则一次函数y=2－2x，y=5－2x的图象之间.

查看试题解析
14. 如图，直线 $l_{1}$ ： $y = x + 2$ 与直线 $l_{2}$ ： $y = k x + b$ 相交于点P（m，4），则方程组 ${\begin{matrix} y = x + 2 \\ y = k x + b \end{matrix}$ 的解是．

查看试题解析

三、解答题

15. 在平面直角坐标系中，一次函数y=kx+2的图象经过点（2，1）．

(1)、求k的值，并画出该函数的图象；

(2)、若y=kx+2的图象与y=x+5的图象相交于点P，试判断P点的象限并说明理由．

查看试题解析
16. 已知：如图1，在平面直角坐标系中，直线 $l_{1}$ ： $y = - x + 4$ 与坐标轴分别相交于点A、B与 $l_{2}$ ： $y = \frac{1}{3} x$ 相交于点C．

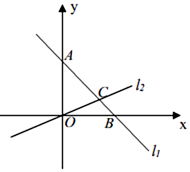(1)、求点C的坐标；

(2)、若平行于y轴的直线 $x = a$ 交于直线 $l_{1}$ 于点E，交直线 $l_{2}$ 于点D，交x轴于点M，且 $E D = 2 D M$ ，求a的值；

查看试题解析
17. 如图，直线y₁=-2x+3和直线y₂=mx-3分别交y轴于点A、B ，两直线交于点C（1，n）.

(1)、求 m、n的值；

(2)、求△ABC的面积；

(3)、请根据图象直接写出：当 y₁＜y₂时，自变量x的取值范围．

查看试题解析
18. 如图，直线l₁过点A(0，4)与点D(4，0)，直线l₂：y＝ $\frac{1}{2}$ x＋1与x轴交于点C，两直线l₁ ， l₂相交于点B．

(1)、求直线l₁的函数表达式；

(2)、求点B的坐标；

(3)、求△ABC的面积．

查看试题解析
19. 如图，直线y= $\frac{1}{2}$ x+2交x轴于点A，交y轴于点B，点P（x，y）是线段AB上一动点（与A，B不重合），△PAO的面积为S，求S与x的函数关系式，并写出自变量的取值范围.

查看试题解析
20. 在平面直角坐标系中有两条直线： $y = \frac{3}{5} x + \frac{9}{5}$ 和 $y = - \frac{3}{2} x + 6$ ，它们的交点为点P，且它们与轴的交点分别为A、B.

(1)、在同一坐标系中作出两条直线的图象；

(2)、求A、B两点的坐标和△PAB的面积.

查看试题解析
21. 两个一次函数的图象如图所示，

(1)、分别求出两个一次函数的解析式；

(2)、求出两个一次函数图象的交点C坐标；

(3)、求这两条直线与y轴围成△ABC的面积．

查看试题解析

沪科版八年级数学上册 12.3 一次函数与二元一次方程 同步练习

一、选择题

二、填空题

三、解答题

沪科版八年级数学上册 12.3 一次函数与二元一次方程同步练习