2018-2019学年数学浙教版八年级上册5.5一次函数的简单应用（2） 同步训练
试卷更新日期：2018-10-19 类型：同步测试
一、选择题
-
1. 已知甲、乙两弹簧的长度y（cm）与所挂物体x（kg）之间的函数解析式分别是y1=k1x+b1 ， y2=k2x+b2 ， 图象如下图所示，当所挂物体质量均为2kg时，甲、乙两弹簧的长度y1与y2的大小关系为（ ）
A、y1＞y2 B、y1=y2 C、y1＜y2 D、不能确定2. 某航空公司规定，旅客乘机所携带行李的运费y（元）与其质量x（kg）由（如图所示）一次函数确定，那么旅客可携带的免费行李的最大质量为（ ）
A、15kg B、20kg C、23kg D、25kg3. 2006年的夏天，某地旱情严重．该地10号，15号的人日均用水量的变化情况如图所示．若该地10号，15号的人均用水量分别为18千克和15千克，并一直按此趋势直线下降．当人日均用水量低于10千克时，政府将向当地居民送水．那么政府应开始送水的号数为（ ）
A、23 B、24 C、25 D、264. 在一次远足活动中，小聪和小明由甲地步行到乙地后原路返回，小明在返回的途中的丙地时发现物品可能遗忘在乙地，于是从丙返回乙地，然后沿原路返回．两人同时出发，步行过程中保持匀速．设步行的时间为t（h），两人离甲地的距离分别为S1（km）和S2（km），图中的折线分别表示S1、S2与t之间的函数关系．则下列说法中正确的是（ ）
A、甲、乙两地之间的距离为20km B、乙、丙两地之间的距离为4km C、小明由甲地出发首次到达乙地的时间为 小时 D、小明乙地到达丙地用了 小时5. 甲、乙两车沿同一平直公路由A地匀速行驶（中途不停留）前往终点B地，甲、乙两车的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示，小红通过图象得出以下4个信息：①甲车速度为60千米/小时；②A、B两地相距240千米；③乙车行驶2小时追上甲车；④乙车由A地到B地共用3小时．上述信息正确的有（ ）个．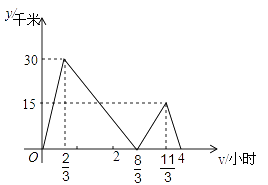
A、1 B、2 C、3 D、4二、填空题
-
6. 某班带队到展览馆参观，并要求作好记录，小亮随队伍步行一段时间后，发现未带笔记本，随即跑步返回拿到笔记本后又以相同的速度追赶队伍，恰好与队伍在同一时间到达展览馆．行程与时间的关系如图所示，其中实线表示队伍的图象，虚线表示小亮的图象，则小亮跑步的速度为米/分钟．
7. 某汽车生产厂对其生产的A型汽车进行耗油量实验，实验中汽车视为匀速行驶．
已知油箱中的余油量y（升）与行驶时间t（小时）的关系如下表，
行驶时间t（时）
0
1
2
3
油箱余油量y（升）
100
84
68
52
与行驶路程x（千米）的关系如图．则A型车在实验中的速度是千米/时．
8. 如图，lA，lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系．若B的自行车不发生故障，保持出发时的速度前进，则与A相遇时，相遇点C的坐标是 ．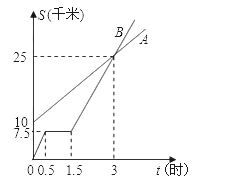
9. 一慢车和一快车沿相同路线从A地到相距120千米的B地，所行地路程与时间的函数图象如图所示，试根据图像，回答下列问题：
(1)、慢车比快车早出发小时，快车比慢车少用小时到达B地；(2)、快车用小时追上慢车；此时相距A地千米。三、解答题
-
10. 小丽一家利用元旦三天驾车到某景点旅游，小汽车出发前油箱有油36L，行驶若干小时后，中途在加油站加油若干升，油箱中余油量Q（L）与行驶时间t（h）之间的关系如图所示，根据图象回答下列问题：
(1)、汽车行驶h后加油，中途加油L；(2)、求加油前油箱余油量Q与行驶时间t之间的函数关系式；
(3)、如果加油站距景点200km，车速为80km/h，要到达目的地，油箱中的油是否够用？请说明理由．
11. 如图所示，直线l1与l2分别表示一种白炽灯和一种节能灯的费用y（费用=灯的售价+电费，单位：元）与照明时间x（h）的函数关系图象，假设两种灯的使用寿命都是2000h，照明效果一样．
(1)、白炽灯和节能灯的售价分别是每只多少元？(2)、求出直线l1与l2的函数解析式．并直接写出x的取值范围．(3)、讨论当照明时间为多少时，两种灯的费用相等？当照明时间为多少时用白炽灯更合算，当照明时间为多少时用节能灯合算．