2018-2019学年数学北师大版八年级上册第四章《一次函数》单元测试卷
试卷更新日期：2018-10-19 类型：单元试卷
一、选择题
-
1. 在平面直角坐标系中，点P（－2，－3）所在的象限是（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 已知点A在x轴的上方，在y轴的左侧，且距离x轴3个单位，且距离y轴4个单位，那么A点的坐标是（ ）
A、(－4，3) B、(4，－3) C、(－3，4) D、( －4， －3)3. 下列函数：下列函数：①y＝－8x；② y＝－ ；③y＝2x－3；④ y＝－8x2＋6；⑤ y＝0.5x－1中，是一次函数的有（ ）
A、1个 B、2个 C、3个 D、4个4. 关于 的一次函数 的图象可能是（ ）A、
B、
C、
D、
5. 一次函数y=kx+b(k≠0)的图象如图所示，当y>0时，x的取值范围是（ ）
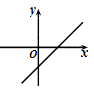A、x<0 B、x>0 C、x<2 D、x>26. 对于一次函数y=-2x+4，下列结论错误的是（ ）
A、函数值随自变量的增大而减小 B、函数的图象不经过第三象限 C、函数的图象向下平移 4 个单位长度得y=-2x 的图象 D、函数的图象与x轴的交点坐标是(0，4)7. 为了鼓励节约用水，按以下规定收取水费：(1)每户每月用水量不超过20立方米，则每立方米水费1.8元；(2)若每户每月用水量超过20立方米，则超过部分每立方米水费3元．设某户一个月所交水费为y(元)，用水量为x(立方米)，则y与x的函数关系用图象表示为（ ）
A、
B、
C、
D、
8. 一家电信公司提供两种手机的月通话收费方式供用户选择，其中一种有月租费，另一种无月租费．这两种收费方式的通话费用y(元)与通话时间x(min)之间的函数关系如图所示．小红根据图象得出下列结论：①l1描述的是无月租费的收费方式；②l2描述的是有月租费的收费方式；③当每月的通话时间为500min时，选择有月租费的收费方式省钱．其中，正确结论的个数是（ ）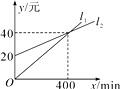
A、0 B、1 C、2 D、39. 如图，把直线y=－2x向上平移后得到直线AB，直线AB经过点(m，n)，且2m＋n=6，则直线AB的解析式是（ ）
A、y=－2x－3 B、y=－2x－6 C、y=－2x＋3 D、y=－2x＋610. 已知点M(1，a)和点N(2，b)是一次函数y=－2x＋1图象上的两点，则a与b的大小关系是（ ）
A、a＞b B、a=b C、a＜b D、以上都不对11. 一次函数y1＝k x＋b与y2＝x＋a的图象如图，则下列结论：①k <0；②a >0；③当x <3 时， y1< y2中，错误的个数是（ ）
A、0 B、1 C、2 D、312. 如图，过点A0 (2，0)作直线l：y＝ x垂直，垂直为点A1 ， 过点A1作A1 A2⊥x轴，垂直为点A2 ， 过点A2作A2 A3⊥l，垂直为点A3 ， ……，这样依次下去，得到一组线段：A0 A1 ， A1 A2 ， A2 A3 ， ……，则线段A2016 A2017的长为（ ）
A、( )2015 B、( )2016 C、( )2017 D、( )2018二、填空题
-
13. 如果点P（3，y1），Q（2，y2）都在一次函数y＝2x－1的图象上，则y1y2 ． （“＞”、“＜”）
14. 若点P(a，4－a)是第一象限的点，则a的取值范围是 ．
15. 直线y=-x与直线y=x+2 与x 轴围成的三角形面积是 ．
16. 过点(－1，7)的一条直线与x轴，y轴分别相交于点A，B，且与直线y=－ x＋1平行．则在线段AB上，横、纵坐标都是整数的点的坐标是 ．
三、解答题
-
17.(1)、分别写出图中点A、B、C的坐标．
(2)、点A（－2，2）和点B（－3，－2）在平面直角坐标系中的位置如图所示．作出线段AB的关于y轴对称的线段A′B′，并写出点A′ 和B′ 的坐标．
18. 已知一次函数y=ax+b的图象经过点A(1，3)且与y=2x-3 平行．
(1)、求出a，b.写出y 与x 的函数关系；
(2)、求当x=-2 时，y的值，当y=10 时，x的值．19. 已知一次函数y=ax+b(1)、当点P(a，b)在第二象限时，直线y=ax+b经过哪几个象限？(2)、如果ab <0，且y随x的增大而增大，则函数的图象不经过哪些象限？
20. 已知一次函数y=kx＋b的图象经过点A(0，2)和点B(－a，3)，且点B在正比例函数y=－3x的图象上．
(1)、求a的值；
(2)、求一次函数的解析式并画出它的图象；(3)、若P(m，y1)，Q(m－1，y2)是这个一次函数图象上的两点，试比较y1与y2的大小．21. 已知一次函数y=mx＋3－m，当m为何值时，
(1)、y随x值的增大而减小；
(2)、一次函数的图象与直线y=－2x平行；(3)、一次函数的图象与x轴交于点(2，0)．求m的值。
22. 我国很多城市水资源缺乏，为了加强居民的节水意识，某市制定了每月用水4吨以内（包括4吨）和用水4吨以上两种收费标准（收费标准：每吨水的价格），某用户每月应交水费y（元）是用水量x（吨）的函数，其函数图象如图所示．
(1)、分别求出当0≤x≤4、x＞4时函数的解析式；
(2)、当0≤x≤4、x＞4时，每吨水的价格分别是多少？
(3)、若某用户该月交水费12.8元，求该户用了多少吨水．
23. 已知A地在B地正南方向 3 千米处，甲、乙两人分别从两地向正北方向匀速直行，他们与A地的距离S(千米)与所行时间t(时)之间的关系如图，其l2表示甲运动 的过程，l1表示乙运动的过程，根据图象回答：
(1)、甲和乙哪一个在A地，哪一个在B地？(2)、追者用多长时间追上被追者？哪一个是追者？(3)、求出表示甲、乙的函数表达式．