2016-2017学年福建省泉州市南安市八年级上学期期末数学试卷

试卷更新日期：2017-03-10 类型：期末考试

进入出卷网下载

一、选择题．

1. 在 $\sqrt{4}$ ，3.14， $\frac{3}{11}$ ， $\sqrt{3}$ ， $\frac{π}{5}$ ，0.66666，这6个数中，无理数共有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 下列算式中，结果等于a⁶的是（）

A、a⁴+a² B、a²+a²+a² C、a²•a³ D、a²•a²•a²

查看试题解析
3. 在下列各组数据中，不能作为直角三角形的三边长的是（）

A、4，5，6 B、6，8，10 C、7，24，25 D、9，12，15

查看试题解析
4. 如图，是某企业1～5月份利润的折线统计图，根据图中信息，下列说法错误的是（）

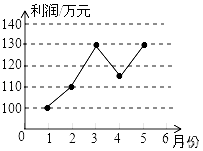A、利润最高是130万 B、利润最低是100万 C、利润增长最快的是2～3月份 D、利润增长最快的是4～5月份

查看试题解析
5. 若（y+3）（y﹣2）=y²+my+n，则m、n的值分别为（　　）

A、m=5，n=6 B、m=1，n=﹣6 C、m=1，n=6 D、m=5，n=﹣6

查看试题解析
6. 下列作图语言中，正确的是（）

A、画直线AB=3cm B、延长线段AB到C，使BC=AB C、画射线AB=5cm D、延长射线OA到B，使AB=OA

查看试题解析
7. 下列命题中，真命题的是（）

A、同位角相等 B、相等的角是对顶角 C、同角的余角相等 D、内错角相等

查看试题解析
8. 用反证法证明“若a＞b＞0，则a²＞b²”，应假设（）

A、a²＜b² B、a²=b² C、a²≤b² D、a²≥b²

查看试题解析
9. 下列式子中，能用平方差公式计算的是（）

A、（﹣x+1）（x﹣1） B、（﹣x﹣1）（x+1） C、（﹣x﹣1）（﹣x+1） D、（x﹣1）（1﹣x）

查看试题解析
10. 如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（）

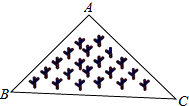A、△ABC的三条中线的交点 B、△ABC三条角平分线的交点 C、△ABC三条高所在直线的交点 D、△ABC三边的中垂线的交点

查看试题解析

二、填空题．

11. 若 $n < \sqrt{11} < n + 1$ ，且n是正整数，则n= ．

查看试题解析
12. 分解因式：mn²+2mn+m= ．

查看试题解析
13. 王老师对本班40名学生的血型作了统计，列出如下的统计表，则本班A型血的人数是人．
组别
A型
B型
AB型
O型
频率
x
0.4
0.15
0.1

查看试题解析
14. 写出命题“内错角相等”的逆命题．

查看试题解析
15. 计算： ${(\frac{1}{3})}^{2016} \times {(- 3)}^{2018}$ = ．

查看试题解析
16. 如图是“赵爽弦图”，由4个全等的直角三角形拼成的图形，若大正方形的面积是13，小正方形的面积是1，设直角三角形较长直角边为a，较短直角边为b，则a+b的值是．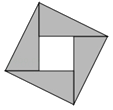

查看试题解析

三、解答题

17. 计算： $\sqrt{16} + | 1 - \sqrt{3} | + \sqrt[3]{- 27}$ ．

查看试题解析
18. 用简便方法计算（要写出运算过程）：

(1)、2017²﹣2016×2018

(2)、198² ．

查看试题解析
19. 先化简，再求值：3a（2a²﹣4a）﹣（12a⁵﹣16a³）÷2a² ，其中a=﹣2．

查看试题解析
20. 如图，已知A，F，E，C在同一直线上，AB∥CD，∠1=∠2，AF=CE．

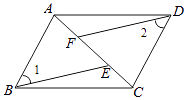(1)、写出图中全等的三角形；

(2)、选择其中一对，说明理由．

查看试题解析
21. 某校八年级数学兴趣小组的同学调查了若干名家长对“初中生带手机上学”现象的看法，统计整理并制作了如下的条形与扇形统计图．依据图中信息，解答下列问题：

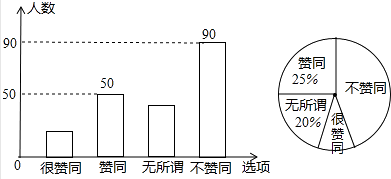(1)、接受这次调查的家长共有人；

(2)、补全条形统计图；

(3)、在扇形统计图中，“很赞同”的家长占被调查家长总数的百分比是；

(4)、在扇形统计图中，“不赞同”的家长部分所对应扇形的圆心角度数是度．

查看试题解析
22. 如图，小明的家D距离大树底部A是9米，一次台风过后，大树在离地面3米的点B处折断，顶端着地处点C在AD上，又知BC恰好等于CD．

(1)、请用直尺和圆规作出点C的位置（保留作图痕迹，不必写作法）；

(2)、求大树折断前高度．

查看试题解析
23. 探究应用：

(1)、计算：（x+1）（x²﹣x+1）=；（2x+y）（4x²﹣2xy+y²）= ．

(2)、上面的乘法计算结果很简洁，你发现了什么规律（公式）？用含a、b的字母表示该公式为：．

(3)、下列各式能用第（2）题的公式计算的是．

A、（m+2）（m²+2m+4） B、（m+2n）（m²﹣2mn+2n²） C、（3+n）（9﹣3n+n²） D、（m+n）（m²﹣2mn+n²）

查看试题解析
24. 如图，△ABC中，AC=BC=10cm，AB=12cm，点D是AB的中点，连结CD，动点P从点A出发，沿A→C→B的路径运动，到达点B时运动停止，速度为每秒2cm，设运动时间为t秒．

(1)、求CD的长；

(2)、当t为何值时，△ADP是直角三角形？

(3)、直接写出：当t为何值时，△ADP是等腰三角形？

查看试题解析
25.
如图①所示，四边形ABCD是长方形，将长方形ABCD折叠，点B恰好落在AD边上的点E处，折痕为FG，如图②所示：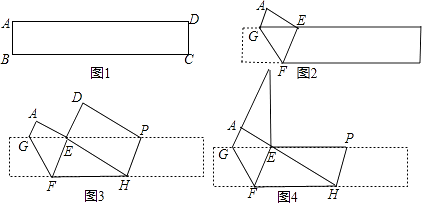

(1)、图②中，证明：GE=EF；

(2)、将图②折叠，点C与点E重合，折痕为PH，如图③所示，当∠FEH=90°时：
①当EF=5，EH=12时，求长方形ABCD的面积；
②将图③中的△PED绕着点E旋转，使点D与点A重合，点P与点M重合，
如图④，求证：△GEM≌△FEH．

查看试题解析

组别	A型	B型	AB型	O型
频率	x	0.4	0.15	0.1