2016-2017学年安徽省安庆市八年级上学期期末数学试卷
试卷更新日期:2017-03-10 类型:期末考试
一、选择题
-
1. 下列表述中,能确定准确位置的是( )A、教室第三排 B、湖心南路 C、南偏东40° D、东经112°,北纬51°2. 我国主要银行的商标设计基本上都融入了中国古代钱币的图案,如图是我国四个银行的商标图案,其中是轴对称图形的有( )
 A、①②③ B、①②④ C、①③④ D、②③④3. 在下列四组点中,可以在同一个正比例函数图象上的一组点是( )A、(2,﹣3),(﹣4,6) B、(﹣2,3),(4,6) C、(﹣2,﹣3),(4,﹣6) D、(2,3),(﹣4,6)4. 下列命题是真命题的是( )A、若直线y=﹣kx﹣2过第一、三、四象限,则k<0 B、三角形三条角平分线的交点到三个顶点的距离相等 C、如果∠A=∠B,那么∠A和∠B是对顶角 D、如果a•b=0,那么a=05. 设三角形三边之长分别为3,8,1﹣2a,则a的取值范围为( )A、﹣6<a<﹣3 B、﹣5<a<﹣2 C、﹣2<a<5 D、a<﹣5或a>26.
A、①②③ B、①②④ C、①③④ D、②③④3. 在下列四组点中,可以在同一个正比例函数图象上的一组点是( )A、(2,﹣3),(﹣4,6) B、(﹣2,3),(4,6) C、(﹣2,﹣3),(4,﹣6) D、(2,3),(﹣4,6)4. 下列命题是真命题的是( )A、若直线y=﹣kx﹣2过第一、三、四象限,则k<0 B、三角形三条角平分线的交点到三个顶点的距离相等 C、如果∠A=∠B,那么∠A和∠B是对顶角 D、如果a•b=0,那么a=05. 设三角形三边之长分别为3,8,1﹣2a,则a的取值范围为( )A、﹣6<a<﹣3 B、﹣5<a<﹣2 C、﹣2<a<5 D、a<﹣5或a>26.如图,把直线l沿x轴正方向向右平移2个单位得到直线l′,则直线l′的解析式为( )
 A、y=2x+4 B、y=﹣2x﹣2 C、y=2x﹣4 D、y=﹣2x+27.
A、y=2x+4 B、y=﹣2x﹣2 C、y=2x﹣4 D、y=﹣2x+27.如图,已知∠1=2,AC=AD,从下列条件:①AB=AE②BC=ED③∠C=∠D④∠B=∠E中添加一个条件,能使△ABC≌△AED的有( )
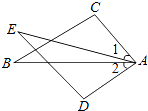 A、1个 B、2个 C、3个 D、4个8. 如图,∠ADB=∠AEC=100°,∠BAD=50°,BD=EC,则∠C=( )
A、1个 B、2个 C、3个 D、4个8. 如图,∠ADB=∠AEC=100°,∠BAD=50°,BD=EC,则∠C=( )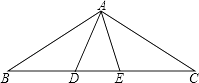 A、20° B、50° C、30° D、40°9. 如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )
A、20° B、50° C、30° D、40°9. 如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( ) A、①③ B、①②④ C、①③④ D、①②③④10. 如图,点A,B,C在一次函数y=﹣2x+m的图象上,它们的横坐标依次为﹣1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
A、①③ B、①②④ C、①③④ D、①②③④10. 如图,点A,B,C在一次函数y=﹣2x+m的图象上,它们的横坐标依次为﹣1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( ) A、1 B、3 C、3(m﹣1) D、
A、1 B、3 C、3(m﹣1) D、二、填空题
-
11. 已知y﹣2与x成正比例,当x=1时,y=5,那么y与x的函数关系式是 .12. 如图,在△ABC中,∠ABC=48°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠ABE=°.
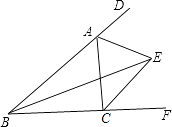 13. 在直角坐标系中,点A(﹣1,2),点P(0,y)为y轴上的一个动点,当y=时,线段PA的长得到最小值.14. 如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是(请将所有正确结论的序号都填上).
13. 在直角坐标系中,点A(﹣1,2),点P(0,y)为y轴上的一个动点,当y=时,线段PA的长得到最小值.14. 如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是(请将所有正确结论的序号都填上).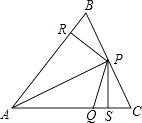
三、解答题
-
15.
△ABC在平面直角坐标系中的位置如图所示.
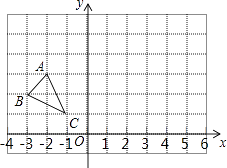 (1)、在图中画出△ABC与关于y轴对称的图形△A1B1C1 , 并写出顶点A1、B1、C1的坐标;(2)、若将线段A1C1平移后得到线段A2C2 , 且A2(a,2),C2(﹣2,b),求a+b的值.16. 已知:如图,P是OC上一点,PD⊥OA于D,PE⊥OB于E,F、G分别是OA、OB上的点,且PF=PG,DF=EG.
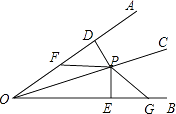
(1)、在图中画出△ABC与关于y轴对称的图形△A1B1C1 , 并写出顶点A1、B1、C1的坐标;(2)、若将线段A1C1平移后得到线段A2C2 , 且A2(a,2),C2(﹣2,b),求a+b的值.16. 已知:如图,P是OC上一点,PD⊥OA于D,PE⊥OB于E,F、G分别是OA、OB上的点,且PF=PG,DF=EG.求证:OC是∠AOB的平分线.
 17.
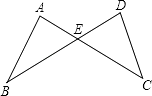
17.如图,AC=BD,AB=DC.求证:∠B=∠C.
 18.
18.在同一平面直角坐标系内画一次函数y1=﹣x+4和y2=2x﹣5的图象,根据图象求:
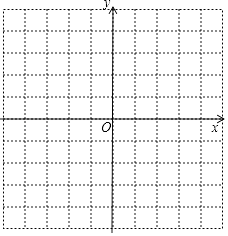 (1)、方程﹣x+4=2x﹣5的解;(2)、当x取何值时,y1>y2?19. 如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为一边作等边三角形CDE,连接AE.
(1)、方程﹣x+4=2x﹣5的解;(2)、当x取何值时,y1>y2?19. 如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为一边作等边三角形CDE,连接AE.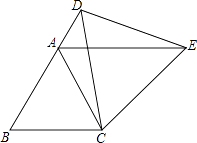 (1)、求证:△CBD≌△CAE.(2)、判断AE与BC的位置关系,并说明理由.20. 已知一次函数y=kx+b的自变量的取值范围是﹣3≤x≤6,相应的函数值的取值范围是﹣5≤y≤﹣2,求这个一次函数的解析式.21. 某公司需要购买甲、乙两种商品共150件,甲、乙两种商品的价格分别为600元和1000元.且要求乙种商品的件数不少于甲种商品件数的2倍.设购买甲种商品x件,购买两种商品共花费y元.(1)、请求出y与x的函数关系式及x的取值范围.(2)、试利用函数的性质说明,当购买多少件甲种商品时,所需要的费用最少?22.
(1)、求证:△CBD≌△CAE.(2)、判断AE与BC的位置关系,并说明理由.20. 已知一次函数y=kx+b的自变量的取值范围是﹣3≤x≤6,相应的函数值的取值范围是﹣5≤y≤﹣2,求这个一次函数的解析式.21. 某公司需要购买甲、乙两种商品共150件,甲、乙两种商品的价格分别为600元和1000元.且要求乙种商品的件数不少于甲种商品件数的2倍.设购买甲种商品x件,购买两种商品共花费y元.(1)、请求出y与x的函数关系式及x的取值范围.(2)、试利用函数的性质说明,当购买多少件甲种商品时,所需要的费用最少?22.解答题
 (1)、如图1,以△ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG,连接EG,试判断△ABC与△AEG面积之间的关系,并说明理由.(2)、园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米.23.
(1)、如图1,以△ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG,连接EG,试判断△ABC与△AEG面积之间的关系,并说明理由.(2)、园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米.23.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
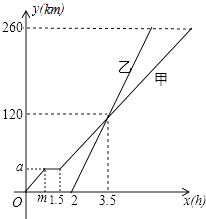 (1)、求出图中m,a的值;(2)、求出甲车行驶路程y(km)与时间x(h)的函数解析式,并写出相应的x的取值范围;(3)、当乙车行驶多长时间时,两车恰好相距50km.
(1)、求出图中m,a的值;(2)、求出甲车行驶路程y(km)与时间x(h)的函数解析式,并写出相应的x的取值范围;(3)、当乙车行驶多长时间时,两车恰好相距50km.