2018-2019学年数学九年级上学期期中模拟试卷（浙江专版）

试卷更新日期：2018-10-18 类型：期中考试

进入出卷网下载

一、选择题

1. 下列函数不属于二次函数的是（）

A、y=（x﹣1）（x+2） B、y= $\frac{1}{2}$ （x+1）² C、y=1﹣ $\sqrt{3}$ x² D、y=2（x+3）²﹣2x²

查看试题解析
2. 已知二次函数 $y = - {(x - h)}^{2}$ ( $h$ 为常数)，当自变量 $x$ 的值满足 $2 \leq x \leq 5$ 时，与其对应的函数值 $y$ 的最大值为-1，则 $h$ 的值为（）

A、3或6 B、1或6 C、1或3 D、4或6

查看试题解析
3. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图像如图所示，下列结论正确的是（）

A、 $a b c > 0$ B、 $2 a + b < 0$ C、 $3 a + c < 0$ D、 $a x^{2} + b x + c - 3 = 0$ 有两个不相等的实数根

查看试题解析
4. 设直线 $x = 2$ 是函数（a，b，c是 $y = a x^{2} + b x + c$ 常数，a＞0）的图象的对称轴，下列不符合题意的是（）

A、若m＞3，则(m-1)a+b＞0 B、若m＞3，则(m-1)a+b＜0 C、若m＜3，则(m+1)a+b＞0 D、若m＜3，则(m+1)a+b＜0

查看试题解析
5. 用一根长为50 cm的铁丝弯成一个长方形，设这个长方形的一边长为x（cm），它的面积为y（cm²），则y与x之间的函数关系式为（）

A、y＝－x²＋50x B、y＝x²－50x C、y＝－x²＋25x D、y＝－2x²＋25

查看试题解析
6. 一个均匀的正方体木块，每个面上都是分别标有1、3、5、7、9、11，任意掷出正方体木块，朝上的数字为偶数的可能性是（）

A、很可能 B、不可能 C、不太可能 D、可能

查看试题解析
7. 已知二次函数y=x²﹣x+ $\frac{1}{4}$ m﹣1的图象与x轴有交点，则m的取值范围是（）

A、m≤5 B、m≥2 C、m＜5 D、m＞2

查看试题解析
8. 抛物线y=ax²+bx+c的对称轴为直线x=﹣1，部分图象如图所示，下列判断中：
①abc＞0；②b²﹣4ac＞0；③9a﹣3b+c=0；④若点（﹣0.5，y₁），（﹣2，y₂）均在抛物线上，则y₁＞y₂；⑤5a﹣2b+c＜0．其中正确的个数有（）

A、2 B、3 C、4 D、5

查看试题解析
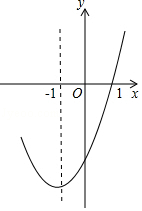9. 若二次函数 $y = (2 - m) x^{2} + m x - 1$ 的图像是开口向上的抛物线，则 $m$ 的取值范围是（）．

A、 $m > 0$ B、 $m > 2$ C、 $m < 0$ D、 $m < 2$

查看试题解析
10. 一个两位数，它的十位数字是3，个位数字是抛掷一枚质地均匀的骰子（六个面分别有数字1—6）朝上一面的数字。任意抛掷这枚骰子一次，得到的两位数是3的倍数的概率等于（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析

二、填空题

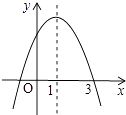
11. 已知二次函数y=ax²+bx+c的图象如图所示，对称轴为直线x=1，则下列结论正确的有．
①abc＞0②方程ax²+bx+c=0的两个根是x₁=﹣1，x₂=3③2a+b=0④当x＞0时，y随x的增大而减小

查看试题解析
12. 如图，线段 $A B$ 的长为2， $C$ 为 $A B$ 上一个动点，分别以 $A C$ 、 $B C$ 为斜边在 $A B$ 的同侧作两个等腰直角三角形 $Δ A C D$ 和 $Δ B C E$ ，那么 $D E$ 长的最小值是.

查看试题解析
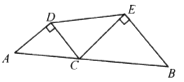13. 不等式x²+ax+b≥0（a≠0）的解集为全体实数，假设f（x）=x²+ax+b，若关于x的不等式f（x）＜c的解集为（m，m+6），则实数c的值为

查看试题解析
14. 在如图所示的图案中，黑白两色的直角三角形都全等．甲、乙两人将它作为一个游戏盘，游戏规则是：按一定距离向盘中投镖一次，扎在黑色区域为甲胜，扎在白色区域为乙胜．这个游戏公平吗？请填上你的正确判断：．

查看试题解析
15. 抛物线y＝ax² ， y＝bx² ， y＝cx²的图象如图所示，则a，b，c的大小关系是．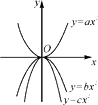

查看试题解析
16. 如图4所示的是桥梁的两条钢缆具有相同的抛物线形状．按照图中建立的直角坐标系，右面的一条抛物线的解析式为y=x²－4x+5表示，而且左右两条抛物线关于y轴对称，则左面钢缆的表达式为．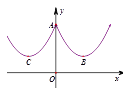

查看试题解析

三、解答题

17. 在同一坐标系中，画出函数y₁＝2x² ， y₂＝2(x－2)²与y₃＝2(x＋2)²的图象，并说明y₂ ， y₃的图象与y₁＝2x²的图象的关系．

查看试题解析
18. 已知二次函数y=ax²﹣2ax+c的图象与x轴交于A、B两点（A左B右），与y轴正半轴交于点C，AB=4，OA=OC，求：二次函数的解析式．

查看试题解析
19. 如图，抛物线y=ax²+4ax+4与x轴仅有一个公共点，经过点A的直线交该抛物线于点C，交y轴于点B，且点B是线段AC的中点，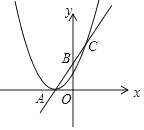

(1)、求该抛物线的解析式；

(2)、求直线AC的解析式．

查看试题解析
20. 一只不透明的袋子中装有4个质地、大小均相同的小球，这些小球分别标有数字3，4，5，x.甲、乙两人每次同时从袋中各随机摸出1个球，并计算摸出的这2个小球上数字之和，记录后都将小球放回袋中搅匀，进行重复试验.试验数据如下表.
摸球
总次数
10
20
30
60
90
120
180
240
330
450
“和为8”出
现的次数
2
10
13
24
30
37
58
82
110
150
“和为8”出
现的频率
0.20
0.50
0.43
0.40
0.33
0.31
0.32
0.34
0.33
0.33

(1)、10次试验“和为8”出现的频率是， 20次试验“和为8”出现的频率是， 450次试验“和为8”出现的频率是；

(2)、如果试验继续进行下去，根据上表数据，估计出现“和为8”的概率是.

查看试题解析
21. 二次函数y=ax²＋bx＋c(a≠0)的图象如图所示，根据图象解答下列问题．

(1)、写出方程ax²＋bx＋c＝0的两个根；

(2)、写出不等式ax²＋bx＋c＞0的解集；

(3)、写出y随x的增大而减小的自变量x的取值范围；

(4)、若方程ax²＋bx＋c＝k有两个不相等的实数根，求k的取值范围．

查看试题解析
22. 为传播奥运知识，小刚就本班学生对奥运知识的了解程度进行了一次调查统计：A：熟悉，B：了解较多，C：一般了解．图1和图2是他采集数据后，绘制的两幅不完整的统计图，请你根据图中提供的信息解答以下问题：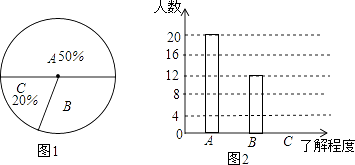

(1)、求该班共有多少名学生；

(2)、在条形图中，将表示“一般了解”的部分补充完整；

(3)、在扇形统计图中，计算出“了解较多”部分所对应的圆心角的度数；

(4)、如果全年级共1000名同学，请你估算全年级对奥运知识“了解较多”的学生人数．

查看试题解析
23. 已知关于x的一元二次方程x²+（k﹣5）x+1﹣k=0（其中k为常数）.

(1)、求证无论k为何值，方程总有两个不相等实数根；

(2)、已知函数y=x²+（k﹣5）x+1﹣k的图象不经过第三象限，求k的取值范围；

(3)、若原方程的一个根大于3，另一个根小于3，求k的最大整数值.

查看试题解析
24. 如图1，地面BD上两根等长立柱AB，CD之间悬挂一根近似成抛物线y= $\frac{1}{10}$ x²﹣ $\frac{4}{5}$ x+3的绳子．

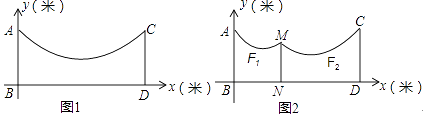(1)、求绳子最低点离地面的距离；

(2)、因实际需要，在离AB为3米的位置处用一根立柱MN撑起绳子（如图2），使左边抛物线F₁的最低点距MN为1米，离地面1.8米，求MN的长；

(3)、将立柱MN的长度提升为3米，通过调整MN的位置，使抛物线F₂对应函数的二次项系数始终为 $\frac{1}{4}$ ，设MN离AB的距离为m，抛物线F₂的顶点离地面距离为k，当2≤k≤2.5时，求m的取值范围．

查看试题解析