2018-2019学年数学八年级上学期期中模拟试卷（浙江专版）

试卷更新日期：2018-10-18 类型：期中考试

进入 出卷网 下载

一、选择题

  • 1. 如图所示，AB∥CD，AB=CD，BE=DF，则图中的全等三角形有（   ）

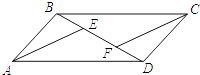    A、2对 B、3对 C、4对 D、5对

    查看试题解析

  • 2. 如图，CE⊥AB，DF⊥AB，垂足分别为E、F，AC∥DB，且AC=BD，那么Rt△AEC≌Rt△BFD的理由是（   ）

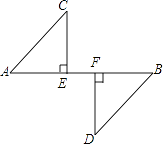    A、SSS B、AAS C、SAS D、HL

    查看试题解析

  • 3. 如图，已知△ABC的六个元素，则下面甲、乙、丙三个三角形中和△ABC全等的图形是（   ）

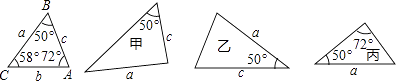    A、甲和乙 B、乙和丙 C、只有乙 D、只有丙

    查看试题解析

  • 4. 三角形一边上的高和这边上的中线重合，则这个三角形一定是（ ）

    A、锐角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形

    查看试题解析

  • 5. 已知等腰△ABC的周长为18 cm，BC＝8 cm，若△ABC与△A′B′C′全等，则△A′B′C′的腰长等于（ ）．
    A、8 cm B、2 cm或8 cm C、5 cm D、8 cm或5 cm

    查看试题解析

  • 6. 如图①是长方形纸带， ∠DEF=α ，将纸带沿 EF 折叠成图②，再沿 BF 折叠成图③，则图③中的 ∠CFE 的度数是（   ）.

    A、2α B、90°+2α C、180°−2α D、180°−3α

    查看试题解析

  • 7. 下列命题的逆命题是真命题的是（   ）
    A、对顶角相等 B、如果两个角是直角那么这两个角相等 C、全等三角形的对应角等 D、两直线平行，内错角相等

    查看试题解析

  • 8. 如图，已知线段AB，以下作图不可能的是（      ）


    A、在AB上取一点C，使AC=BC B、在AB的延长线上取一点C，使BC=AB C、在BA的延长线上取一点C，使BC=AB D、在BA的延长线上取一点C，使BC=2AB

    查看试题解析

  • 9. 如图，在4×4方格中，以AB为一边，第三个顶点也在格点上的等腰三角形可以作出（   ）

    A、7个 B、6个 C、4个 D、3个

    查看试题解析

  • 10. 已知△ABC的三边长分别为a，b，c，且满足（a﹣5）2+|b﹣12|+ c−13 =0，则△ABC（   ）
    A、不是直角三角形 B、是以a为斜边的直角三角形 C、是以b为斜边的直角三角形 D、是以c为斜边的直角三角形

    查看试题解析

二、填空题

  • 11. 如果三角形三个外角度数之比为4：2：3，则这个三角形的各外角度数分别为 ．

    查看试题解析

  • 12. “全等三角形的对应角相等”的逆命题是 ，这个逆命题是命题（填“真”、“假”）。

    查看试题解析

  • 13.

    在△ABC中，∠B，∠C的平分线交于点O，若∠BOC=132°，则∠A=度.

    查看试题解析

  • 14. 判定两直角三角形全等的各种条件：（1）一锐角和一边对应相等（2）两边对应相等（3）两锐角对应相等．其中能得到两个直角三角形全等的条件是

    查看试题解析

  • 15. 如图，在Rt△ABC中，D，E为斜边AB上的两个点，且BD=BC，AE=AC，则∠DCE的大小为（度）．

    查看试题解析

  • 16. 如图， DE⊥AB 于E， DF⊥AC 于F，若 BD=CD ， BE=CF ，则下列结论： ①DE=DF ； ②AD 平分 ∠BAC ； ③AE=AD ； ④AC-AB=2BE 中正确的是 ．

    ③④

    查看试题解析

三、解答题

  • 17. 如图，已知△ABC，求作一点P，使P到∠A的两边的距离相等，且PA=PB．

    要求：尺规作图，并保留作图痕迹．（不要求写作法）

    查看试题解析

  • 18. 上午8时，一条船从海岛A出发，以15海里/时的速度向正北航行，10时到达海岛B处，从A，B望灯塔C，测得∠NAC=43°，∠NBC=86°，问海岛B与灯塔C相距多远？

    查看试题解析

  • 19. 如图，在△ABC中，∠ABC的平分线BF与△ABC的外角平分线CF  相交于点F，过F作DF∥BC，交AB于D，交AC于E。

    (1)、写出图中所有的等腰三角形，并选择其中一个说明理由。
    (2)、直接写出BD，CE，DE之间的数量关系。
    (3)、若DE=5cm，CE=8cm，BF=24cm，求△BDF的面积。

    查看试题解析

  • 20. 已知：四边形ABCD中，AC⊥BC，AB=17，BC=8，CD=12，DA=9；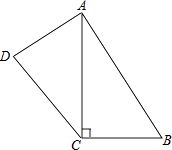

    (1)、求AC的长；
    (2)、求四边形ABCD的面积．

    查看试题解析

  • 21. 如图， △ABC ≌ △DEF ， ∠A=33∘ ， ∠E=57∘ ， CE=5cm ．

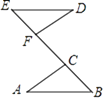    (1)、求线段BF的长；
    (2)、试判断DF与BE的位置关系，并说明理由．

    查看试题解析

  • 22. 如图①，点A，E，F，C在同一直线上，AE＝CF，过点E，F分别作ED⊥AC，FB⊥AC，AB＝CD．

    (1)、若BD与EF交于点G，试证明BD平分EF；
    (2)、若将△DEC沿AC方向移动到图②的位置，其他条件不变，上述结论是否仍然成立？请说明理由．

    查看试题解析

  • 23. 如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高。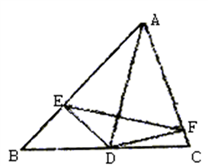


    (1)、求证：AD垂直平分EF。
    (2)、若AB+AC=16，S△ABC=24，∠EDF=120°，求AD的长。

    查看试题解析

  • 24. 在▱ABCD中，E是AD上一点，AE=AB，过点E作直线EF，在EF上取一点G，使得∠EGB=∠EAB，连接AG．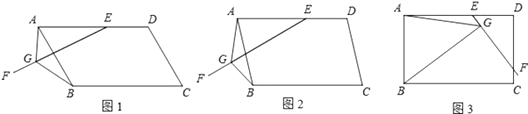

    (1)、如图1，当EF与AB相交时，若∠EAB=60°，求证：EG=AG+BG；
    (2)、如图2，当EF与AB相交时，若∠EAB=α（0°＜α＜90°），请你直接写出线段EG、AG、BG之间的数量关系（用含α的式子表示）；
    (3)、如图3，当EF与CD相交时，且∠EAB=90°，请你写出线段EG、AG、BG之间的数量关系，并证明你的结论．

    查看试题解析