2017年云南省曲靖市罗平县中考数学一模试卷
试卷更新日期：2017-03-09 类型：中考模拟
一、选择题）
-
1. ﹣2016的相反数是（ ）A、﹣2016 B、2016 C、﹣ D、2. 下列运算正确的是（ ）A、x3+x2=x5 B、2x3•x2=2x6 C、（3x3）2=9x6 D、x6÷x3=x23. “十二五”期间，将新建保障性住房约37000000套，用于解决中低收入和新参加工作的大学生住房的需求，把37000000用科学记数法表示应是（ ）A、37×106 B、3.7×106 C、3.7×107 D、0.37×1084. 下列银行标志中，既不是中心对称图形也不是轴对称图形的是（ ）A、
B、
C、
D、
5. 下列命题中，错误的是（ ）A、矩形的对角线互相平分且相等 B、对角线互相垂直的矩形是正方形 C、等腰梯形同一底上的两个角相等 D、对角线互相垂直的四边形是菱形6. 某校九年级数学模拟测试中，六名学生的数学成绩如下（单位：分）：110，106，109，111，108，110，下列关于这组数据描述正确的是（ ）A、众数是110 B、方差是16 C、平均数是109.5 D、极差是67. 如图，△ABC中，∠A=30°，∠C=90°，AB的垂直平分线交AC于D点，交AB于E点，则下列结论错误的是（ ）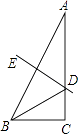
A、DE=DC B、AD=DB C、AD=BC D、BC=AE8. 一个圆锥的母线长为10，侧面展开图是半圆，则圆锥的侧面积是（ ）A、100π B、50π C、20π D、10π二、填空题
-
9. 若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根，则k的取值范围是 ．10. 函数y= 自变量的取值范围是 ．11. 把抛物线y=x2的图象向右平移3个单位，再向下平移2个单位，所得图象的解析式为 ．12. 已知点A的坐标为（﹣2，3），则点A关于原点对称的点B的坐标为 ．13. 如图，⊙P内含于⊙O，⊙O的弦AB切⊙P于点C，且AB∥OP．若阴影部分的面积为16π，则弦AB的长为 ．
14. 如图，一条抛物线y=﹣x（x﹣2）（0≤x≤2）的一部分，记为C1 ， 它与x轴交于O，A1两点，将C1绕点A1旋转180°得到C2 ， 交x轴于点A2 ， ；将C2绕点A2旋转180°得到C3 ， 交x轴于A3；…如此进行下去，直至得到C6 ， 若点P（2017，y）在抛物线Cn上，则y= ．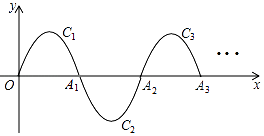
三、解答题
-
15. |﹣1|+（π﹣3.14）0﹣（﹣ ）﹣1﹣ ．16. 解下列方程或不等式组(1)、用配方法解方程：x2﹣x=3x+5(2)、解不等式组： ，并判断﹣1， 这两个数是否为该不等式组的解．17. 先化简，再求值：（ ）÷ ，其中x是方程x2﹣2x﹣2=0的根．18. 已知二次函数y=2x2﹣mx﹣m2(1)、求证：对于任意实数m，二次函数y=2x2﹣mx﹣m2的图象与x轴总有公共点；(2)、若这个二次函数图象与x轴有两个公共点A，B，且B点坐标为（1，0），求A点坐标．19. 如图，△ABC各顶点的坐标分别是A（﹣2，﹣4），B（0，﹣4），C（1，﹣1）．
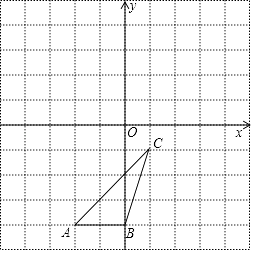(1)、在图中画出△ABC关于原点对称的△AB1C1；(2)、在图中画出△ABC绕原点C逆时针旋转90°后的△A2B2C2；(3)、在（2）的条件下，AC边扫过的面积是 ．20. 如图，在Rt△ABC中，∠BAC=90°，O是AB边上的一点，以OA为半径的⊙O与边BC相切于点E．
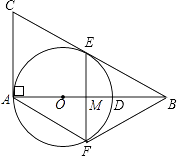(1)、若AC=6，BC=10，求⊙O的半径．(2)、过点E作弦EF⊥AB于M，连接AF，若∠F=2∠B，求证：四边形ACEF是菱形．21. 如图，正方形ABCD的边长为6，E，F分别是AB，BC边上的点，且∠EDF=45°，将△DAE绕点D逆时针旋转90°，得到△DCM．
(1)、求证：EF=FM．(2)、当AE=2时，求EF的长．22. 曲靖市某楼盘准备以每平方米4000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，为了加快资金周转，房地产开发商对价格经过两次下调后，决定以每平方米3240元的均价开盘销售．(1)、求平均每次下调的百分率．(2)、某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9.9折销售；②不打折，送两年物业管理费，物业管理费是每平方米每月1.4元，请问哪种方案更优惠？23.如图，抛物线y=﹣x2+bx+c与x轴交于A（1，0），B（﹣3，0）两点．
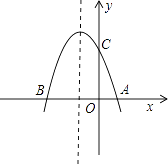(1)、求该抛物线的解析式；(2)、设（1）中的抛物线交y轴与C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由；(3)、在（1）中的抛物线上的第二象限上是否存在一点P，使△PBC的面积最大？若存在，求出点P的坐标及△PBC的面积最大值；若没有，请说明理由．