2017年上海市松江区中考数学一模试卷

试卷更新日期：2017-03-09 类型：中考模拟

进入出卷网下载

一、选择题：

1. 已知在Rt△ABC中，∠C=90°，如果BC=2，∠A=α，则AC的长为（）

A、2sinα B、2cosα C、2tanα D、2cotα

查看试题解析
2. 下列抛物线中，过原点的抛物线是（）

A、y=x²﹣1 B、y=（x+1）² C、y=x²+x D、y=x²﹣x﹣1

查看试题解析
3. 小明身高1.5米，在操场的影长为2米，同时测得教学大楼在操场的影长为60米，则教学大楼的高度应为（）

A、45米 B、40米 C、90米 D、80米

查看试题解析
4. 已知非零向量 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ ，下列条件中，不能判定 $\vec{a}$ ∥ $\vec{b}$ 的是（）

A、 $\vec{a}$ ∥ $\vec{c}$ ， $\vec{b}$ ∥ $\vec{c}$ B、 $| \vec{a} | = 2 | \vec{b} |$ C、 $\vec{a}$ = $- 2 \vec{b}$ D、 $\vec{a}$ = $2 \vec{c}$ ， $\vec{b}$ = $\vec{c}$

查看试题解析
5. 如图，在▱ABCD中，点E是边BA延长线上的一点，CE交AD于点F．下列各式中，错误的是（）

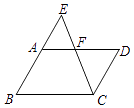A、 $\frac{A E}{A B} = \frac{F E}{F C}$ B、 $\frac{A E}{A B} = \frac{A F}{D F}$ C、 $\frac{A E}{A B} = \frac{A F}{B C}$ D、 $\frac{A E}{B E} = \frac{A F}{B C}$

查看试题解析
6. 如图，已知在△ABC中，cosA= $\frac{1}{3}$ ，BE，CF分别是AC，AB边上的高，联结EF，那么△AEF和△ABC的周长比为（）

A、1：2 B、1：3 C、1：4 D、1：9

查看试题解析

二、填空题：

7. 已知 $\frac{a}{b} = \frac{3}{4}$ ，则 $\frac{2 a}{a + b}$ 的值为．

查看试题解析
8. 计算：（ $\vec{m}$ ﹣3 $\vec{n}$ ）﹣ $\frac{1}{2}$ （ $\vec{m}$ +2 $\vec{n}$ ）= ．

查看试题解析
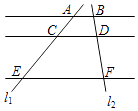
9. 已知抛物线y=（k﹣1）x²+3x的开口向下，那么k的取值范围是．

查看试题解析
10. 把抛物线y=x²向右平移4个单位，所得抛物线的解析式为．

查看试题解析
11. 已知在△ABC中，∠C=90°，sinA= $\frac{3}{4}$ ，BC=6，则AB的长是．

查看试题解析
12. 如图，已知AB∥CD∥EF，它们依次交直线l₁、l₂于点A、C、E和点B、D、F，如果AC：CE=3：5，BF=9，那么DF= ．

查看试题解析
13. 已知点A（2，y₁）、B（5，y₂）在抛物线y=﹣x²+1上，那么y₁y₂ ．（填“＞”、“=”或“＜”）

查看试题解析
14. 已知抛物线y=ax²+bx+c过（﹣1，1）和（5，1）两点，那么该抛物线的对称轴是直线．

查看试题解析
15. 在△ABC中，AB=AC=5，BC=8，AD⊥BC，垂足为D，BE是△ABC 的中线，AD与BE相交于点G，那么AG的长为．

查看试题解析
16. 在一个距离地面5米高的平台上测得一旗杆底部的俯角为30°，旗杆顶部的仰角为45°，则该旗杆的高度为米．（结果保留根号）

查看试题解析
17. 如图，在Rt△ABC中，∠ACB=90°，BC=3，AC=4，AB的垂直平分线DE交BC的延长线于点E，则CE的长为．

查看试题解析
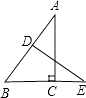18. 如图，在△ABC中，∠ACB=90°，AB=9，cosB= $\frac{2}{3}$ ，把△ABC绕着点C旋转，使点B与AB边上的点D重合，点A落在点E，则点A，E之间的距离为．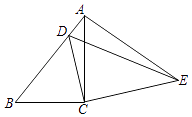

查看试题解析

三、解答题：

19. 计算： $\frac{\sin 60^{\circ} + 3 \tan 30^{\circ} \cdot \cos 60^{\circ}}{(2 \cos 45^{\circ} - 1) \cot 30^{\circ}}$ ．

查看试题解析
20. 如图，已知点D是△ABC的边BC上一点，且BD= $\frac{1}{2}$ CD，设 $\vec{A B}$ = $\vec{a}$ ， $\vec{B C}$ = $\vec{b}$ ．

(1)、求向量 $\vec{A D}$ （用向量 $\vec{a}$ 、 $\vec{b}$ 表示）；

(2)、求作向量 $\vec{A C}$ 在 $\vec{a}$ 、 $\vec{b}$ 方向上的分向量．
（不要求写作法，但要指出所作图中表示结论的向量）

查看试题解析
21. 如图，已知AC∥BD，AB和CD相交于点E，AC=6，BD=4，F是BC上一点，S_△_BEF：S_△_EFC=2：3．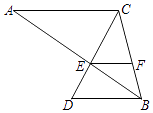

(1)、求EF的长；

(2)、如果△BEF的面积为4，求△ABC的面积．

查看试题解析
22. 某大型购物商场在一楼和二楼之间安装自动扶梯AC，截面如图所示，一楼和二楼地面平行（即AB所在的直线与CD平行），层高AD为8米，∠ACD=20°，为使得顾客乘坐自动扶梯时不至于碰头，A、B之间必须达到一定的距离．
（参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）

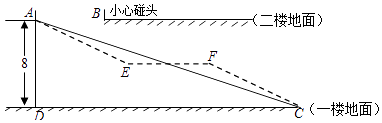(1)、要使身高2.26米的姚明乘坐自动扶梯时不碰头，那么A，B之间的距离至少要多少米？（精确到0.1米）

(2)、如果自动扶梯改为由AE，EF，FC三段组成（如图中虚线所示），中间段EF为平台（即EF∥DC），AE段和FC段的坡度i=1：2，求平台EF的长度．（精确到0.1米）

查看试题解析
23. 如图，Rt△ABC中，∠ACB=90°，D是斜边AB上的中点，E是边BC上的点，AE与CD交于点F，且AC²=CE•CB．

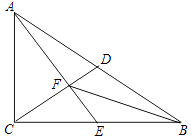(1)、求证：AE⊥CD；

(2)、连接BF，如果点E是BC中点，求证：∠EBF=∠EAB．

查看试题解析
24.
如图，抛物线y=﹣x²+bx+c过点B（3，0），C（0，3），D为抛物线的顶点．

(1)、求抛物线的解析式以及顶点坐标；

(2)、点C关于抛物线y=﹣x²+bx+c对称轴的对称点为E点，联结BC，BE，求∠CBE的正切值；

(3)、点M是抛物线对称轴上一点，且△DMB和△BCE相似，求点M坐标．

查看试题解析
25.
如图，已知四边形ABCD是矩形，cot∠ADB= $\frac{3}{4}$ ，AB=16．点E在射线BC上，点F在线段BD上，且∠DEF=∠ADB．

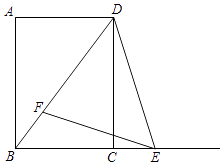(1)、求线段BD的长；

(2)、设BE=x，△DEF的面积为y，求y关于x的函数关系式，并写出函数定义域；

(3)、当△DEF为等腰三角形时，求线段BE的长．

查看试题解析