2017年上海市青浦区中考数学一模试卷
试卷更新日期：2017-03-09 类型：中考模拟
一、选择题：
-
1. 在下列各数中，属于无理数的是（ ）A、4 B、 C、 D、2. 已知a＞b，下列关系式中一定正确的是（ ）A、a2＜b2 B、2a＜2b C、a+2＜b+2 D、﹣a＜﹣b3. 一次函数y=kx﹣1（常数k＜0）的图象一定不经过的象限是（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 抛物线y=2x2+4与y轴的交点坐标是（ ）A、（0，2） B、（0，﹣2） C、（0，4） D、（0，﹣4）5. 顺次连结矩形四边中点所得的四边形一定是（ ）A、菱形 B、矩形 C、正方形 D、等腰梯形6. 如图，在梯形ABCD中，AD∥BC，对角线AC与BD相交于点O，如果S△ACD：S△ABC=1：2，那么S△AOD：S△BOC是（ ）
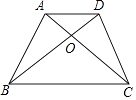A、1：3 B、1：4 C、1：5 D、1：6二、填空题：
-
7. 函数y= 的定义域是 ．8. 方程 =2的根是 ．9. 若关于x的一元二次方程x2﹣2x+m=0有实数根，则m的取值范围是 ．10. 从点数为1、2、3的三张扑克牌中随机摸出两张牌，摸到的两张牌的点数之积为素数的概率是 ．11. 将抛物线y=x2+4x向下平移3个单位，所得抛物线的表达式是 ．12. 如果点A（﹣2，y1）和点B（2，y2）是抛物线y=（x+3）2上的两点，那么 y1y2 ． （填“＞”、“=”、“＜”）13. 如果一个多边形的内角和是它的外角和的2倍，那么这个多边形的边数为 ．14. 点G是△ABC的重心，GD∥AB，交边BC于点D，如果BC=6，那么CD 的长是 ．15. 已知在△ABC中，点D在边AC上，且AD：DC=2：1．设 = ， = ．那么 = ． （用向量 、 的式子表示）16. 如图，在△ABC中，∠C=90°，AC=3，BC=2，边AB的垂直平分线交AC边于点D，交AB边于点E，联结DB，那么tan∠DBC的值是 ．
17. 如图，在平行四边形ABCD中，点E在边AD上，联结CE并延长，交对角线BD于点F，交BA的延长线于点G，如果DE=2AE，那么CF：EF：EG= ．
18. 如图，已知△ABC，将△ABC绕点A顺时针旋转，使点C落在边AB上的点E处，点B落在点D处，连接BD，如果∠DAC=∠DBA，那么 的值是 ．
三、解答题：
-
19. 计算： ÷（a﹣1）+ ．20. 解方程组： ．21. 已知：如图，在平面直角坐标系xOy中，反比例函数y= 的图象与正比例函数y=kx（k≠0）的图象相交于横坐标为2的点A，平移直线OA，使它经过点B（3，0），与y轴交于点C．
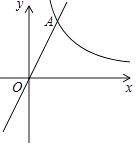(1)、求平移后直线的表达式；(2)、求∠OBC的余切值．22. 某校兴趣小组想测量一座大楼AB的高度．如图6，大楼前有一段斜坡BC，已知BC的长为12米，它的坡度i=1： ．在离C点40米的D处，用测角仪测得大楼顶端A的仰角为37°，测角仪DE的高为1.5米，求大楼AB的高度约为多少米？（结果精确到0.1米）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75， ≈1.73．）
23. 已知：如图，在四边形ABCD中，AB∥CD，对角线AC、BD交于点E，点F在边AB上，连接CF交线段BE于点G，CG2=GE•GD．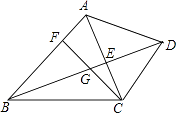
(1)、求证：∠ACF=∠ABD；(2)、连接EF，求证：EF•CG=EG•CB．24.已知：如图，在平面直角坐标系xOy中，抛物线y=ax2﹣4ax+1与x轴的正半轴交于点A和点B，与y轴交于点C，且OB=3OC，点P是第一象限内的点，连接BC，△PBC是以BC为斜边的等腰直角三角形．
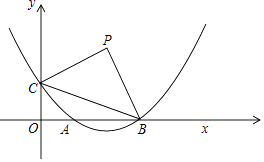(1)、求这个抛物线的表达式；(2)、求点P的坐标；(3)、点Q在x轴上，若以Q、O、P为顶点的三角形与以点C、A、B为顶点的三角形相似，求点Q的坐标．25.已知：如图，在菱形ABCD中，AB=5，联结BD，sin∠ABD= ．点P是射线BC上的一个动点（点P不与点B重合），联结AP，与对角线BD相交于点E，联结EC．
(1)、求证：AE=CE；(2)、当点P在线段BC上时，设BP=x，△PEC的面积为y，求y关于x的函数解析式，并写出它的定义域；(3)、当点P在线段BC的延长线上时，若△PEC是直角三角形，求线段BP的长．