2017年上海市普陀区中考数学一模试卷

试卷更新日期：2017-03-09 类型：中考模拟

进入出卷网下载

一、选择题

1. “相似的图形”是（）

A、形状相同的图形 B、大小不相同的图形 C、能够重合的图形 D、大小相同的图形

查看试题解析
2. 下列函数中，y关于x的二次函数是（）

A、y=2x+1 B、y=2x（x+1） C、y= $\frac{2}{x^{2}}$ D、y=（x﹣2）²﹣x²

查看试题解析
3. 如图，直线l₁∥l₂∥l₃ ，直线AC分别交l₁、l₂、l₃与点A、B、C，直线DF分别交l₁、l₂、l₃与点D、E、F，AC与DF相交于点H，如果AH=2，BH=1，BC=5，那么 $\frac{D E}{E F}$ 的值等于（）

A、 $\frac{1}{5}$ B、 $\frac{1}{3}$ C、 $\frac{2}{5}$ D、 $\frac{3}{5}$

查看试题解析
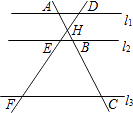4. 抛物线y=﹣x²+bx+c上部分点的横坐标x，纵坐标y的对应值如下表所示：
x
…
﹣2
﹣1
0
1
2
…
y
…
0
4
6
6
4
…
从上表可知，下列说法中，错误的是（）

A、抛物线于x轴的一个交点坐标为（﹣2，0） B、抛物线与y轴的交点坐标为（0，6） C、抛物线的对称轴是直线x=0 D、抛物线在对称轴左侧部分是上升的

查看试题解析
5. 如图，在四边形ABCD中，如果∠ADC=∠BAC，那么下列条件中不能判定△ADC和△BAC相似的是（）

A、∠DAC=∠ABC B、AC是∠BCD的平分线 C、AC²=BC•CD D、 $\frac{A D}{A B}$ = $\frac{D C}{A C}$

查看试题解析
6. 下列说法中，错误的是（）

A、长度为1的向量叫做单位向量 B、如果k≠0，且 $\vec{a}$ ≠ $\vec{0}$ ，那么k $\vec{a}$ 的方向与 $\vec{a}$ 的方向相同 C、如果k=0或 $\vec{a}$ = $\vec{0}$ ，那么k $\vec{a}$ = $\vec{0}$ D、如果 $\vec{a}$ = $\frac{5}{2}$ $\vec{c}$ ， $\vec{b}$ = $\frac{1}{2}$ $\vec{c}$ ，其中 $\vec{c}$ 是非零向量，那么 $\vec{a}$ ∥ $\vec{b}$

查看试题解析

二、填空题

7. 如果x：y=4：3，那么 $\frac{x - y}{y}$ = ．

查看试题解析
8. 计算：3 $\vec{a}$ ﹣4（ $\vec{a}$ + $\vec{b}$ ）= ．

查看试题解析
9. 如果抛物线y=（m﹣1）x²的开口向上，那么m的取值范围是．

查看试题解析
10. 抛物线y=4x²﹣3x与y轴的交点坐标是．

查看试题解析
11. 若点A（3，n）在二次函数y=x²+2x﹣3的图象上，则n的值为．

查看试题解析
12. 已知线段AB的长为10厘米，点P是线段AB的黄金分割点，那么较长的线段AP的长等于厘米．

查看试题解析
13. 利用复印机的缩放功能，将原图中边长为5厘米的一个等边三角形放大成边长为20厘米的等边三角形，那么放大前后的两个三角形的周长比是．

查看试题解析
14. 已知点P在半径为5的⊙O外，如果设OP=x，那么x的取值范围是．

查看试题解析
15. 如果港口A的南偏东52°方向有一座小岛B，那么从小岛B观察港口A的方向是．

查看试题解析
16. 在半径为4厘米的圆面中，挖去一个半径为x厘米的圆面，剩下部分的面积为y平方厘米，写出y关于x的函数解析式：（结果保留π，不要求写出定义域）

查看试题解析
17. 如果等腰三角形的腰与底边的比是5：6，那么底角的余弦值等于．

查看试题解析
18. 如图，DE∥BC，且过△ABC的重心，分别与AB，AC交于点D，E，点P是线段DE上一点，CP的延长线交AB于点Q，如果 $\frac{D P}{D E}$ = $\frac{1}{4}$ ，那么S_△_DPQ：S_△_CPE的值是．

查看试题解析

三、解答题

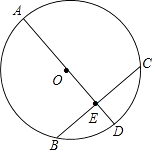
19. 计算：cos²45°+ $\frac{\cos 30^{\circ}}{2 \sin 60^{\circ} + 1}$ ﹣ $\sqrt{3}$ •tan30°．

查看试题解析
20. 如图，已知AD是⊙O的直径，BC是⊙O的弦，AD⊥BC，垂足为点E，AE=BC=16，求⊙O的直径．

查看试题解析
21. 如图，已知向量 $\vec{O A}$ ， $\vec{O B}$ ， $\vec{O P}$ ．

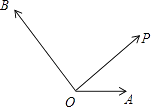(1)、求做：向量 $\vec{O P}$ 分别在 $\vec{O A}$ ， $\vec{O B}$ 方向上的分向量 $\vec{O D}$ ， $\vec{O E}$ ：（不要求写作法，但要在图中明确标出向量 $\vec{O D}$ 和 $\vec{O E}$ ）．

(2)、如果点A是线段OD的中点，联结AE、交线段OP于点Q，设 $\vec{O A}$ = $\vec{a}$ ， $\vec{O P}$ = $\vec{p}$ ，那么试用 $\vec{a}$ ， $\vec{p}$ 表示向量 $\vec{P E}$ ， $\vec{Q E}$ （请直接写出结论）

查看试题解析
22. 一段斜坡路面的截面图如图所示，BC⊥AC，其中坡面AB的坡比i₁=1：2，现计划削坡放缓，新坡面的坡角为原坡面坡脚的一半，求新坡面AD的坡比i₂（结果保留根号）

查看试题解析
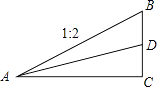23. 已知：如图，在四边形ABCD中，∠BAD=∠CDA，AB=DC= $\sqrt{a b}$ ，CE=a，AC=b，求证：

(1)、△DEC∽△ADC；

(2)、AE•AB=BC•DE．

查看试题解析
24.
如图，已知在平面直角坐标系xOy中，点A（4，0）是抛物线y=ax²+2x﹣c上的一点，将此抛物线向下平移6个单位后经过点B（0，2），平移后所得的新抛物线的顶点记为C，新抛物线的对称轴与线段AB的交点记为P．

(1)、求平移后所得到的新抛物线的表达式，并写出点C的坐标；

(2)、求∠CAB的正切值；

(3)、如果点Q是新抛物线对称轴上的一点，且△BCQ与△ACP相似，求点Q的坐标．

查看试题解析
25.
如图，在直角三角形ABC中，∠ACB=90°，AB=10，sinB= $\frac{3}{5}$ ，点O是AB的中点，∠DOE=∠A，当∠DOE以点O为旋转中心旋转时，OD交AC的延长线于点D，交边CB于点M，OE交线段BM于点N．

(1)、当CM=2时，求线段CD的长；

(2)、设CM=x，BN=y，试求y与x之间的函数解析式，并写出定义域；

(3)、如果△OMN是以OM为腰的等腰三角形，请直接写出线段CM的长．

查看试题解析

x	…	﹣2	﹣1	0	1	2	…
y	…	0	4	6	6	4	…