2017年上海市闵行区中考数学一模试卷

试卷更新日期：2017-03-09 类型：中考模拟

进入出卷网下载

一、一.选择题

1. 在△ABC中，点D，E分别在边AB，AC上，且DE∥BC，下列结论错误的是（）

A、 $\frac{A D}{B D} = \frac{A E}{C E}$ B、 $\frac{A D}{A B} = \frac{A E}{A C}$ C、 $\frac{D E}{B C} = \frac{A D}{B D}$ D、 $\frac{B D}{A B} = \frac{C E}{A C}$

查看试题解析
2. 在 Rt△ABC中，∠C=90°，CD⊥AB，垂足为点D，下列四个三角比正确的是（）

A、sinA= $\frac{A C}{A B}$ B、cosA= $\frac{A D}{A C}$ C、tanA= $\frac{C D}{B D}$ D、cotA= $\frac{C D}{A D}$

查看试题解析
3. 将二次函数y=2x²﹣1的图象向下平移3个单位后所得图象的函数解析式为（）

A、y=2（x﹣3）²﹣1 B、y=2（x+3）²﹣1 C、y=2x²+4 D、y=2x²﹣4

查看试题解析
4. 已知 $\vec{b}$ =﹣2 $\vec{a}$ ，那么下列判断错误的是（）

A、| $\vec{b}$ |=2| $\vec{a}$ | B、2 $\vec{a} + \vec{b} = 0$ C、 $\vec{b} ∥ \vec{a}$ D、 $\vec{b} \neq \vec{a}$

查看试题解析
5. 一位篮球运动员跳起投篮，篮球运行的高度y（米）关于篮球运动的水平距离x（米）的函数解析式是y=﹣ $\frac{1}{5}$ （x﹣2.5）²+3.5．已知篮圈中心到地面的距离3.05米，如果篮球运行高度达到最高点之后能准确投入篮圈，那么篮球运行的水平距离为（）

A、1米 B、2米 C、4米 D、5米

查看试题解析
6. 如图，已知D是△ABC中的边BC上的一点，∠BAD=∠C，∠ABC的平分线交边AC于E，交AD于F，那么下列结论中错误的是（）

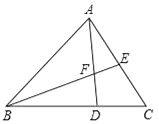A、△BDF∽△BEC B、△BFA∽△BEC C、△BAC∽△BDA D、△BDF∽△BAE

查看试题解析

二、二.填空题

7. 已知：3a=2b，那么 $\frac{2 a + 3 b}{2 a - 3 b}$ = ．

查看试题解析
8. 计算：（ $\frac{1}{2}$ $\vec{a}$ + $\vec{b}$ ）﹣（ $\frac{7}{2}$ $\vec{a}$ ﹣2 $\vec{b}$ ）= ．

查看试题解析
9. 如果地图上A，B两处的图距是4cm，表示这两地实际的距离是20km，那么实际距离500km的两地在地图上的图距是 cm．

查看试题解析
10. 二次函数y=﹣ $\frac{1}{2}$ x²+5的图象的顶点坐标是．

查看试题解析
11. 已知抛物线y=x²﹣4x+3，如果点P（0，5）与点Q关于该抛物线的对称轴对称，那么点Q的坐标是．

查看试题解析
12. 已知两个相似三角形的面积之比是1：4，那么这两个三角形的周长之比是．

查看试题解析
13. 已知在Rt△ABC中，∠C=90°，BC=6，sinA= $\frac{2}{3}$ ，那么AB= ．

查看试题解析
14. 已知一斜坡的坡度i=1：2，高度在20米，那么这一斜坡的坡长约为米（精确到0.1米）

查看试题解析
15. 如图，在平行四边形ABCD中，点E在边AB上，联结DE，交对角线AC于点F，如果 $\frac{S_{△ A D F}}{S_{△ D F C}}$ = $\frac{2}{3}$ ，CD=6，那么AE= ．

查看试题解析
16. 如图，△OPQ在边长为1个单位的方格纸中，它们的顶点在小正方形顶点位置，点A，B，C，D，E也是小正方形的顶点，从点A，B，C，D，E中选取三个点所构成的三角形与△OPQ相似，那么这个三角形是．

查看试题解析
17. 2016年3月完工的上海中心大厦是一座超高层地标式摩天大楼，其高度仅次于世界排名第一的阿联酋迪拜大厦，某人从距离地面高度263米的东方明珠球体观光层测得上海中心大厦顶部的仰角是22.3°．已知东方明珠与上海中心大厦的水平距离约为900米，那么上海中心大厦的高度约为米（精确到1米）．（参考数据：sin22.3°≈0.38，cos22.3°≈0.93．tan22.3°≈0.41）

查看试题解析
18. 如图，已知△ABC是边长为2的等边三角形，点D在边BC上，将△ABD沿着直线AD翻折，点B落在点B₁处，如果B₁D⊥AC，那么BD= ．

查看试题解析

三、三.解答题

19. 已知：在平面直角坐标系xOy中，抛物线y=ax²+bx+c经过点A（3，0），B（2，﹣3），C（0，﹣3）

(1)、求抛物线的表达式；

(2)、设点D是抛物线上一点，且点D的横坐标为﹣2，求△AOD的面积．

查看试题解析
20. 如图，在△ABC中，点D，E分别是边AB，AC的中点，设 $\vec{A B}$ = $\vec{a}$ ， $\vec{B C}$ = $\vec{b}$ ．

(1)、求向量 $\vec{C E}$ （用向量 $\vec{a}$ ， $\vec{b}$ 的式子表示）．

(2)、在图中作出向量 $\vec{B E}$ 在向量 $\vec{B A}$ ， $\vec{B C}$ 方向上的分向量（不要求写作法，但要指出所作图中表示结论的向量）．

查看试题解析
21. 如图，在△ABC中，点D是AB边上一点，过点D作DE∥BC，交AC于E，点F是DE延长线上一点，联结AF．

(1)、如果 $\frac{A D}{A B} = \frac{2}{3}$ ，DE=6，求边BC的长；

(2)、如果∠FAE=∠B，FA=6，FE=4，求DF的长．

查看试题解析
22. 如图，电线杆CD上的C处引拉线CE，CF固定电线杆，在离电线杆6米的B处安置测角仪（点B，E，D在同一直线上），在A处测得电线杆上C处的仰角为30°，已知测角仪的高AB=1.5米，BE=2.3米，求拉线CE的长，（精确到0.1米）参考数据 $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73．

查看试题解析
23. 如图，已知在四边形ABCD中，AD∥BC，E为边CB延长线上一点，联结DE交边AB于点F，联结AC交DE于点G，且 $\frac{F G}{G D}$ = $\frac{A D}{C E}$ ．

(1)、求证：AB∥CD；

(2)、如果AD²=DG•DE，求证： $\frac{E G^{2}}{C E^{2}}$ = $\frac{A G}{A C}$ ．

查看试题解析
24. 如图，已知在平面直角坐标系xOy中，二次函数y=﹣x²+mx+n的图象经过点A（3，0），B（m，m+1），且与y轴相交于点C．

(1)、求这个二次函数的解析式并写出其图象顶点D的坐标；

(2)、求∠CAD的正弦值；

(3)、设点P在线段DC的延长线上，且∠PAO=∠CAD，求点P的坐标．

查看试题解析
25.
如图，已知在梯形ABCD中，AD∥BC，AB=AD=5，tan∠DBC= $\frac{3}{4}$ ．点E为线段BD上任意一点（点E与点B，D不重合），过点E作EF∥CD，与BC相交于点F，连接CE．设BE=x，y= $\frac{S_{△ E C F}}{S_{△ B C D}}$ ．

(1)、求BD的长；

(2)、如果BC=BD，当△DCE是等腰三角形时，求x的值；

(3)、如果BC=10，求y关于x的函数解析式，并写出自变量x的取值范围．

查看试题解析