2016年天津市河北区中考数学一模试卷
试卷更新日期:2017-03-09 类型:中考模拟
一、选择题:
-
1. 计算3﹣(﹣6)的结果等于( )A、﹣9 B、﹣3 C、3 D、92. 2cos60°的值等于( )A、1 B、 C、 D、23.
下列图形中,中心对称图形有( )
 A、1个 B、2个 C、3个 D、4个4. 地球绕太阳公转的速度约是110000千米/时,110000用科学记数法表示为( )A、0.11×106 B、11×104 C、1.1×105 D、1.1×1045.
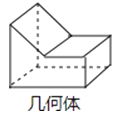
A、1个 B、2个 C、3个 D、4个4. 地球绕太阳公转的速度约是110000千米/时,110000用科学记数法表示为( )A、0.11×106 B、11×104 C、1.1×105 D、1.1×1045.如图所示为某几何体的示意图,该几何体的左视图应为( )
 A、
A、 B、
B、 C、
C、 D、
D、 6. 判断 的值会介于下列哪两个整数之间( )A、17,18 B、18,19 C、19,20 D、21,227. 计算 的值是( )A、0 B、2 C、﹣1 D、18. 如图,过正五边形ABCDE的顶点A作直线l∥BE,则∠1的度数为( )
6. 判断 的值会介于下列哪两个整数之间( )A、17,18 B、18,19 C、19,20 D、21,227. 计算 的值是( )A、0 B、2 C、﹣1 D、18. 如图,过正五边形ABCDE的顶点A作直线l∥BE,则∠1的度数为( )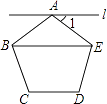 A、30° B、36° C、38° D、45°9. 若关于x、y的二元一次方程组 的解满足x+y>1,则实数k的取值范围是( )A、k<0 B、k<﹣1 C、k<﹣2 D、k<﹣310. 如图,矩形ABCD中,M为CD中点,分别以B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P,若∠PBC=70°,则∠MPC的度数为( )
A、30° B、36° C、38° D、45°9. 若关于x、y的二元一次方程组 的解满足x+y>1,则实数k的取值范围是( )A、k<0 B、k<﹣1 C、k<﹣2 D、k<﹣310. 如图,矩形ABCD中,M为CD中点,分别以B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P,若∠PBC=70°,则∠MPC的度数为( ) A、55° B、40° C、35° D、20°11. 一次函数y1=kx+b(k≠0)与反比例函数y2= ,在同一直角坐标系中的图象如图所示,若y1<y2 , 则x的取值范围是( )
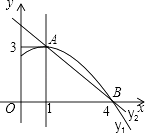
A、55° B、40° C、35° D、20°11. 一次函数y1=kx+b(k≠0)与反比例函数y2= ,在同一直角坐标系中的图象如图所示,若y1<y2 , 则x的取值范围是( ) A、﹣2<x<0或x>1 B、x>1 C、x<﹣2或0<x<1 D、﹣2<x<112. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论:
A、﹣2<x<0或x>1 B、x>1 C、x<﹣2或0<x<1 D、﹣2<x<112. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论:①当x<1时,有y1<y2;
②a+b+c=m+n;
③b2﹣4ac=﹣12a;
④若m﹣n=﹣5,则B点坐标为(4,0)
其中正确的是( )
 A、① B、①② C、①②③ D、①②③④
A、① B、①② C、①②③ D、①②③④二、填空题:
-
13. 计算:2x3•(﹣3x)2的结果等于 .14. 在一次函数y=kx+2中,若y随x的增大而增大,则它的图象不经过第象限.15. 在一个不透明的盒子里,装有4个黑球和若干个白球,它们除颜色外没有任何其他区别,摇匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复,共摸球50次,其中10次摸到黑球,则估计盒子中大约有白球个.16. 命题“对顶角相等”的“条件”是 .17. 如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,若ED:DC=2:3,△DEF的面积为8,则平行四边形ABCD的面积为 .
 18. 如图,将△ABP放在每个小正方形的边长为1的网格中,点A、B、P均落在格点上.
18. 如图,将△ABP放在每个小正方形的边长为1的网格中,点A、B、P均落在格点上.
(1)、△ABP的面积等于;(2)、若线段AB水平移动到A′B′,且使PA′+PB′最短,请你在如图所示的网格中,用直尺画出A′B′,并简要说明画图的方法(不要求证明).
三、解答题:
-
19. 解不等式组 ,并写出不等式组的整数解.20. 某教师就中学生对课外数阅读状况进行了一次问卷调查,并根据调查结果绘制了中学生每学期阅读课外书籍数量的统计图(不完整).设x表示阅读书籍的数量(x为正整数,单位:本),其中A:1≤x≤2;B:3≤x≤4;C:5≤x≤6;D:x≥7.请你根据两幅图提供的信息解答下列问题:
 (1)、本次共调查了多少名学生?(2)、补全条形统计图,并判断中位数在哪一组;(3)、计算扇形统计图中扇形D的圆心角的度数.21. 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.
(1)、本次共调查了多少名学生?(2)、补全条形统计图,并判断中位数在哪一组;(3)、计算扇形统计图中扇形D的圆心角的度数.21. 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C. (1)、求证:CB∥PD;(2)、若BC=6,sin∠P= ,求AB的值.22. 如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.( 取1.73,结果保留整数)
(1)、求证:CB∥PD;(2)、若BC=6,sin∠P= ,求AB的值.22. 如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.( 取1.73,结果保留整数) 23. 某市为美化城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配成A、B两种园艺造型共60个,摆放于主干街道的两侧,搭配每个造型所需花卉数量的情况如下表所示,结合上述信息,解答下列问题:
23. 某市为美化城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配成A、B两种园艺造型共60个,摆放于主干街道的两侧,搭配每个造型所需花卉数量的情况如下表所示,结合上述信息,解答下列问题:造型花卉
甲
乙
A
80
40
B
50
70
(1)、符合题意的搭配方案有几种?(2)、如果搭配一个A种造型的成本为600元,搭配一个B种造型的成本为800元,试说明选用那种方案成本最低?最低成本为多少元?24. 已知:如图①,在平面直角坐标系xOy中,A(0,5),C( ,0),AOCD为矩形,AE垂直于对角线OD于E,点F是点E关于y轴的对称点,连AF、OF. (1)、求AF和OF的长;(2)、如图②,将△OAF绕点O顺时针旋转一个角α(0°<α<180°),记旋转中的△OAF为△OA′F′,在旋转过程中,设A′F′所在的直线与线段AD交于点P,与线段OD交于点Q,是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时点P坐标;若不存在,请说明理由.25. 如图,已知二次函数y=ax2+ 的图象与y轴交于点A(0,4),与x轴交于点B,C,点C坐标为(8,0),连AB,AC,点N在线段BC上运动(不与点B,C重合)过点N作NM∥AC,交AB于点M.
(1)、求AF和OF的长;(2)、如图②,将△OAF绕点O顺时针旋转一个角α(0°<α<180°),记旋转中的△OAF为△OA′F′,在旋转过程中,设A′F′所在的直线与线段AD交于点P,与线段OD交于点Q,是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时点P坐标;若不存在,请说明理由.25. 如图,已知二次函数y=ax2+ 的图象与y轴交于点A(0,4),与x轴交于点B,C,点C坐标为(8,0),连AB,AC,点N在线段BC上运动(不与点B,C重合)过点N作NM∥AC,交AB于点M. (1)、判断△ABC的形状,并说明理由;(2)、当以点A,M,N为顶点的三角形与以点A,B,O为顶点的三角形相似时,求点N的坐标;(3)、当△AMN面积等于3时,直接写出此时点N的坐标.
(1)、判断△ABC的形状,并说明理由;(2)、当以点A,M,N为顶点的三角形与以点A,B,O为顶点的三角形相似时,求点N的坐标;(3)、当△AMN面积等于3时,直接写出此时点N的坐标.