2016年江苏省无锡市滨湖区中考数学模拟试卷

试卷更新日期：2017-03-09 类型：中考模拟

进入出卷网下载

一、选择题

1. $\frac{1}{3}$ 的相反数是（）

A、﹣ $\frac{1}{3}$ B、3 C、﹣3 D、 $\frac{1}{3}$

查看试题解析
2. 下列计算正确的是（）

A、a²+a²=a⁴ B、（a²）³=a⁵ C、a+2=2a D、（ab）³=a³b³

查看试题解析
3. 已知某种纸一张的厚度约为0.0089cm，用科学记数法表示这个数为（）

A、8.9×10³ B、8.9×10^﹣⁴ C、8.9×10^﹣³ D、89×10^﹣²

查看试题解析
4. 已知一次函数y=kx﹣2k+3的图象与x轴交于点A（3，0），则该图象与y轴的交点的坐标为（）

A、（0，﹣3） B、（0，1） C、（0，3） D、（0，9）

查看试题解析
5. 为调查某班学生每天使用零花钱的情况，张华随机调查了30名同学，结果如下表：
每天使用零花钱（单位：元）
1
2
3
4
5
人数
2
5
8
9
6
则这30名同学每天使用的零花钱的众数和中位数分别是（）

A、4，3 B、4，3.5 C、3.5，3.5 D、3.5，4

查看试题解析
6. 下列命题中，是真命题的为（）

A、四个角相等的四边形是矩形 B、四边相等的四边形是正方形 C、对角线相等的四边形是菱形 D、对角线互相垂直的四边形是平行四边形

查看试题解析
7. 十边形的内角和为（）

A、360° B、1440° C、1800° D、2160°

查看试题解析
8. 如图是一个由多个相同小正方体堆积而成的几何体的俯视图，图中所示数字为该位置小正方体的个数，则这个几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
9. 如图，已知⊙O为△ABC的外接圆，且AB为⊙O的直径，若OC=5，AC=6，则BC长为（）

A、10 B、9 C、8 D、无法确定

查看试题解析
10. 如图，A在O的正北方向，B在O的正东方向，且OA=OB．某一时刻，甲车从A出发，以60km/h的速度朝正东方向行驶，与此同时，乙车从B出发，以40km/h的速度朝正北方向行驶.1小时后，位于点O处的观察员发现甲、乙两车之间的夹角为45°，即∠COD=45°，此时，甲、乙两人相距的距离为（）

A、90km B、50 $\sqrt{2}$ km C、20 $\sqrt{13}$ km D、100km

查看试题解析

二、填空题

11. 若分式 $\frac{x - 1}{x - 3}$ 的值为0，则x=

查看试题解析
12. 分解因式：2x²﹣8= ．

查看试题解析
13. 某公司2月份的利润为160万元，4月份的利润250万元，若设平均每月的增长率x，则根据题意可得方程为．

查看试题解析
14. 已知△ABC中，AC=BC，∠A=80°，则∠B=°．

查看试题解析
15. 如图，已知A（4，0），B（3，3），以OA、AB为边作▱OABC，则若一个反比例函数的图象经过C点，则这个反比例函数的表达式为．

查看试题解析
16. 如图，△ABC三个顶点的坐标分别为A（2，2），B（4，2），C（6，4），以原点O为位似中心，将△ABC缩小为原来的一半，则线段AC的中点P变换后在第一象限对应点的坐标为．

查看试题解析
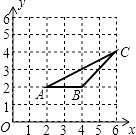17. 甲、乙两工程队分别同时开挖两条600米长的管道，所挖管道长度y（米）与挖掘时间x（天）之间的关系如图所示，则下列说法中：
①甲队每天挖100米；
②乙队开挖两天后，每天挖50米；
③甲队比乙队提前3天完成任务；
④当x=2或6时，甲乙两队所挖管道长度都相差100米．
正确的有．（在横线上填写正确的序号）

查看试题解析
18. 在平面直角坐标系中，点O为坐标原点，A、B、C三点的坐标为（ $\sqrt{3}$ ，0）、（3 $\sqrt{3}$ ，0）、（0，5），点D在第一象限，且∠ADB=60°，则线段CD的长的最小值为．

查看试题解析

三、解答题

19. 解答题

(1)、计算：（ $\frac{1}{3}$ ）⁰+ $\sqrt{27}$ ﹣|﹣3|+tan45°；

(2)、计算：（x+2）²﹣2（x﹣1）．

查看试题解析
20. 解方程组

(1)、解方程组： ${\begin{matrix} 3 x - y = 1 \\ 2 x + 3 y = 8 \end{matrix}$

(2)、解不等式： $\frac{2 x - 1}{3}$ ＜x．

查看试题解析
21. 如图，在▱ABCD中，E是BC的中点，连接AE并延长交DC的延长线于点F．

(1)、求证：AB=CF；

(2)、连接DE，若AD=2AB，求证：DE⊥AF．

查看试题解析
22. 某高校学生会发现同学们就餐时剩余饭菜较多，浪费严重，于是准备在校内倡导“光盘行动”，让同学们珍惜粮食，为了让同学们理解这次活动的重要性，校学生会在某天午餐后，随机调查了部分同学就餐饭菜的剩余情况，并将结果统计后绘制成了如图所示的不完整的统计图．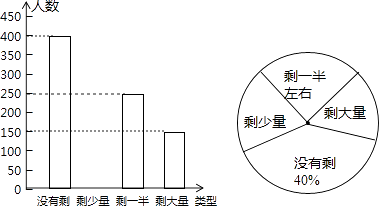

(1)、这次被调查的同学共有名；

(2)、补全条形统计图；

(3)、计算在扇形统计图中剩大量饭菜所对应扇形圆心角的度数；

(4)、校学生会通过数据分析，估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐．据此估算，该校20000名学生一餐浪费的食物可供多少人食用一餐？

查看试题解析
23. 某市今年的信息技术结业考试，采用学生抽签的方式决定自己的考试内容．规定：每位考生先在三个笔试题（题签分别用代码B₁、B₂、B₃表示）中抽取一个，再在三个上机题（题签分别用代码J₁、J₂、J₃表示）中抽取一个进行考试．小亮在看不到题签的情况下，分别从笔试题和上机题中随机地抽取一个题签．

(1)、用树状图或列表法表示出所有可能的结果；

(2)、求小亮抽到的笔试题和上机题的题签代码的下标（例如“B₁”的下标为“1”）为一个奇数一个偶数的概率．

查看试题解析
24. 如图，四边形ABCD 内接于⊙O，BD是⊙O的直径，过点A作⊙O的切线AE交CD的延长线于点E，DA平分∠BDE．

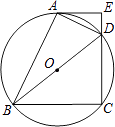(1)、求证：AE⊥CD；

(2)、已知AE=4cm，CD=6cm，求⊙O的半径．

查看试题解析
25. 旅行社为某旅游团包飞机去旅游，其中旅游社的包机费为15000元，旅游团中每人的飞机票按以下方式与旅行社结算；若旅游团的人数在30人或30人以下，飞机票每张收费900元；若旅游团的人数多于30人，则给予优惠，每多1人，机票费每张减少10元，但旅游团的人数最多有75人．设旅游团的人数为x人，每张飞机票价为y元，旅行社可获得的利润为W元．

(1)、写出y与x之间的函数关系式；

(2)、写出W与x之间的函数关系式；

(3)、当旅游团的人数为多少时，旅行社可获得的利润最大？最大利润为多少元？

查看试题解析
26. 如图1、2是底面半径为1cm，母线长为2cm的圆柱体和圆锥体模型．现要用长为2πcm，宽为4cm的长方形彩纸（如图3）装饰圆柱、圆锥模型表面．已知一个圆柱和一个圆锥模型为一套，长方形彩纸共有122张，用这些纸最多能装饰多少套模型呢？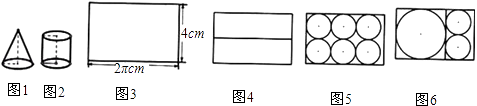
老师：“长方形纸可以怎么裁剪呢？”
学生甲：“可按图4方式裁剪出2张长方形．”
学生乙：“可按图5方式裁剪出6个小圆．”
学生丙：“可按图6方式裁剪出1个大圆和2个小圆．”
老师：尽管还有其他裁剪方法，但为裁剪方便，我们就仅用这三位同学的裁剪方法！

(1)、计算：圆柱的侧面积是cm² ，圆锥的侧面积是cm² ．

(2)、1张长方形彩纸剪拼后最多能装饰个圆锥模型；5张长方形彩纸剪拼后最多能装饰个圆柱体模型．

(3)、求用122张彩纸对多能装饰的圆锥、圆柱模型套数．

查看试题解析
27.
如图（1），∠AOB=45°，点P、Q分别是边OA，OB上的两点，且OP=2cm．将∠O沿PQ折叠，点O落在平面内点C处．

(1)、①当PC∥QB时，求OQ的长度；
②当PC⊥QB时，求OQ的长．

(2)、当折叠后重叠部分为等腰三角形时，求OQ的长．

查看试题解析
28.
如图，经过原点的抛物线y=﹣x²+2mx与x轴的另一个交点为A．点P在一次函数y=2x﹣2m的图象上，PH⊥x轴于H，直线AP交y轴于点C，点P的横坐标为1．（点C不与点O重合）

(1)、如图1，当m=﹣1时，求点P的坐标．

(2)、如图2，当 $0 < m < \frac{1}{2}$ 时，问m为何值时 $\frac{C P}{A P} = 2$ ？

(3)、是否存在m，使 $\frac{C P}{A P} = 2$ ？若存在，求出所有满足要求的m的值，并定出相对应的点P坐标；若不存在，请说明理由．

查看试题解析

每天使用零花钱（单位：元）	1	2	3	4	5
人数	2	5	8	9	6